Расстояние - данная точка
Cтраница 1
Расстояние данной точки до оси вращения равно 60 см. Ротор делает 3000 об / мин. [1]
Здесь г обозначает расстояние данной точки А ( скорость которой определяется) от переменной точки вихревого поля, по которой производится интегрирование; последнее распространяется на все пространство. Вывод уравнения ( 23) сравнительно сложен; поэтому мы его здесь только наметим. [2]
Найти кривую, если расстояние данной точки до любой касательной к этой кривой постоянно. [3]
Следовательно, нужно знать не только расстояние данной точки от той или иной плоскости координат, но и направление, по которому надо это расстояние отложить; для этого координаты точек выражают относительными числами. [4]
Зная зависимость местной линейной скорости и от расстояния данной точки от оси трубы, вычислим ( например графическим методом) интеграл, входящий в уравнение ( 1 - 7), а затем найдем объемную скорость потока. [5]
 |
Векторы линейной скорости v для. различных точек вращающегося тела. [6] |
Величина скорости точки вращающегося тела равна произведению расстояния данной точки от оси вращения на величину угловой скорости тела. [7]
Измеряется зависимость этих величин от координаты х, представляющей расстояние данной точки от фронта ударной волны. [8]
Если проволока достаточно тонка, то зависимостью скорости w от расстояния данной точки кольца от его оси можно пренебречь. [9]
Если проволока достаточно тонка, то зависимостью скорости w от расстояния данной точки кольца от его оси можно пренебречь. [10]
Если проволока достаточно тонка, то зависимостью скорости w от расстояния данной точки кольца до его оси можно пренебречь. [11]
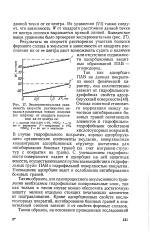 |
Экспериментальная зависимость скорости растворения металла в различных точках полоски ( по ширине от квадрата расстояния их от центра ее. [12] |
Из уравнения ( VI) также следует, что зависимость WOT квадрата расстояния данной точки от центра полоски выражается прямой линией. [13]
Значение скорости в различных точках внутри вращающейся звезды не одинаково и зависит от расстояния данной точки от оси вращения. Поэтому для точного вычисления кинетической энергии необходимо знать распределение вещества внутри звезды. [14]
Таким образом, численное значение скорости точки вращающегося тела равно произведению угловой скорости на расстояние данной точки от оси вращения. [15]
Страницы: 1 2 3 4