Инвариантное расстояние

Cтраница 1

Инвариантное расстояние х - у определяет в К топологию метрического пространства, согласующуюся со структурой аддитивной грунпы в К ( предложение 3); кроме того, эта топология согласуется со структурой тела в К. [1]

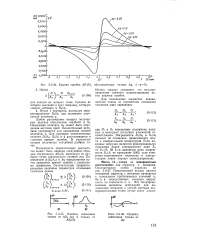Кривая ошибок ДО ( 5, 3. Найти.| Ошибки, зависящие. [2]

Метод И - схема с инвариантным расстоянием для структур с потерями. [3]

Здесь д / - r r - инвариантное расстояние от протона до точки наблюдения в один и тот же момент времени. [4]

Здесь / ( лг дсь) - инвариантное расстояние точки ( /, ) от точки ( / ль) центра заряженной частицы, вычисленное вдоль геодезической, соединяющей эти точки, а б - инвариантный размер частицы. Заметим, что интеграл (8.3.4) по части 2, расположенной внутри горизонта событий, представляет собой энергию поля, находящегося внутри черной дыры, и соответствующий вклад входит как часть в определение полной массы черной дыры. [5]

Здесь ( - г Гд) 1 / 2 - инвариантное расстояние от протона до точки наблюдения. [6]

В криволинейных координатах g v, заданная как функция координат, фиксирует все элементы инвариантного расстояния; таким образом, gw задает метрику. Величина g определяет как координатную систему, так и кривизну пространства. [7]

Если период колебаний в свободной от поля области пространства равен Т, то величина s icT представляет инвариантное расстояние между двумя мировыми точками, соответствующими двум последовательным крайним положениям колеблющегося атома относительно той системы отсчета, в которой он покоится. [8]

В то же время ( см. [2]) расстояние по вариации является единственным ( с точностью до множителя) инвариантным расстоянием, определяемым нормой разности. [9]

Из этих аксиом вытекает, что 1 1 и - а: а: для всех х 6 К. Функция d ( х, у) - х - у есть инвариантное расстояние на аддитивной группе К, и топология, которую оно определяет в Kt согласуется с заданной структурой тела в К. [10]

Наконец, установление того, что у) влечет а), свести к случаю, когда № п ( Un, X) A. N - подгруппа группы G, состоящая из всех элементов, проекции которых с индексом ( k, X) равны нулю для всех X б L и всех / с п; показать, что / - гомеоморфизм пространства Е на подпространство группы G, наделенной групповой топологией, для которой ( Gn) слунсит фундаментальной системой окрестпостой 0; в заключение заметить, что топология группы G может быть задана инвариантным расстоянием, превращающим G в ультраметрическое пространство. [11]

Есть только еще одно условие. Мы должны потребовать, чтобы результат был релятивистски инвариантным. Так что в качестве расстояния мы должны взять инвариантное расстояние между двумя точками в пространстве-времени. [12]

Согласно основному положению общей теории относительности, мировая линия свободной частицы в четырехмерном пространстве - времени является геодезической линией. Аффинная связность определенным образом выражает геометрические свойства пространства, а следовательно, связана также с гравитацией и с динамическими свойствами. Но для описания геометрии недостаточно одних геодезических. Нужен еще способ, позволяющий сравнивать расстояния вдоль различных геодезических. Для этого нам нужно установить, каким образом определяется инвариантное расстояние между каждой парой точек пространства. [13]

Страницы: 1