Совершенно аналогичные рассуждения

Cтраница 2

При сополимеризации двух мономеров А и В совершенно аналогичные рассуждения приводят к вероятностям различных последовательностей мономерных единиц Уравнения ( 12, 13, 15) автоматически переходят в уравнения для концентрации различных монад, диад и триад мономерных звеньев после замены m и г на А и В. [16]

Последнюю можно считать равной работе ионизации, если получающиеся ионы находятся в нормальном, а не в возбужденном состоянии; во всяком случае следует считать, что энергия активации и работа ионизации изменяются, по крайней мере, параллельно друг другу. Совершенно аналогичные рассуждения применимы и к диссоциации органических оснований. [17]

Случай 2: игрок II имеет выигрывающую стратегию в игре GA. Совершенно аналогичные рассуждения показывают, что в этом случае уже множество О - А включает некоторый конус. Доказательство леммы Мартина закончено. [18]

Выражения (1.5) и (1.6) были получены для плосконапряженного состояния. Но совершенно аналогичные рассуждения, хотя и требующие более сложных преобразований, справедливы для общего случая трехмерного напряженного состояния. При этом появляется третье главное напряжение 03, и вместо заключения о существовании двух взаимно перпендикулярных направлений, в которых экстремальны нормальные напряжения и отсутствуют касательные, необходимо сформулировать вывод о существовании ( в трехмерном пространстве) трех таких взаимно перпендикулярных направлений. Далее, при обобщении понятия об инвариантах на трехмерное напряженное состояние формулы (1.5) и (1.6) несколько изменятся из-за появления новых компонент напряжений. [19]

В докладе о статье Эрмита Лиувилль сравнил деление аргументов эллиптических и абелевых функций с делением аргументов тригонометрических функций, например при выражении синуса кратного угла через синус простого угла, и отметил, что подобные задачи ( деления аргумента) всегда значительно сложнее, чем задачи сложения или умножения аргументов ( см. с. Эрмит установил, что совершенно аналогичные рассуждения применимы и к другим классам ультраэллиптических функций. [20]

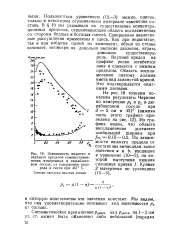Зависимость нижнего и верхнего пределов самовоспламенения, измеренных в дюрабаксо-вом сосуде, от содержания водорода в смеси при 467 С. [21]

Совершенно аналогичные рассуждения применимы и здесь. [22]

Наше определение У на пространстве У является, очевидно, сужением этого определения. Мы уже отмечали, что определение преобразования Фурье - Шварца согласуется с данным элементарным определением, когда это преобразование применяется к функциям из У. Совершенно аналогичные рассуждения показывают, что эта согласованность имеет место и для интегрируемых функций вообще. Действительно, каждая интегрируемая функция f является в - 5 1 oS 1 ( R, ji) пределом последовательности ( ип) элементов из У. [23]

Сделанный вывод мы получили, исходя из утверждения, что малые части системы распределены по энергиям во времени канонически. Совершенно аналогичные рассуждения применимы к ансамблю, изображающему распределение вероятностей системы в данный, достаточно удаленный момент времени. При этом следует исходить из того, что малые части распределены в данный момент по энергиям согласно каноническому вероятностному закону. [24]

Таким образом, наиболее вероятным является такое распределение состояний, которое допускает наибольшее число перестановок отдельных значений между отдельными молекулами без изменения этих средних значений. Я уже показывал в первой части, § 6, как математическое условие этого для одноатомных газовых молекул приводит к макс-велловскому распределению состояний. Не входя в это более подробно, я все же хочу заметить, что справедливость приведенных там рассуждений отнюдь не ограничивается случаем одноатомных молекул; совершенно аналогичные рассуждения можно провести и для случая сложных молекул. [25]

Изображенный случай относится к сильно легированным ( вырожденным) р - и - областям, так что уровни Ферми в обеих областях находятся в пределах разрешенных зон При равновесии эти уровни для электронов и для дырок совпадают, если к переходу приложено напряжение V в прямом направлении, то положение уровней Ферми на двух контактах различается на величину энергии, соответствующей этому напряжению Если проводимости объема р - и - областей велики, то все напряжение оказывается приложенным непосредственно к переходу. В каждой из двух областей вдали от перехода носители тока находятся в тепловом равновесии, и их распределение можно описать с помощью квазиуровня Ферми Однако в области перехода равновесие отсутствует, и статистика заполнения состояний в этой области должна рассматриваться отдельно для зоны проводимости и валентной зоны. Прежде всего если речь идет о зоне проводимости, то при тепловом равновесии электроны в р - и - областях находятся в равновесии друг с другом и их распределение описывается статистикой Ферми - Дирака. При включении прямого смещения возникает диффузионный поток электронов через переход, который стремится поднять квазиуровень Ферми для электронов в р-области до его уровня в - области. Инжектированные электроны после диффундирования на небольшое расстояние ( диффузионную длину) рекомбинируют с дырками, в результате возникает стационарное состояние, при котором скорость рекомбинации электронов в точности сбалансирована скоростью их инжекции Совершенно аналогичные рассуждения применимы и к распределению дырок в валентной зоне, так что в стационарном состоянии положение квазиуровней Ферми для двух типов носителей в области перехода меняется, как это показано на фиг. Основные носители, конечно, вытягиваются из контакта, чтобы обеспечить условие нейтральности. [26]

Первые производные от функций щ по времени - это скорости. Напряжения выражаются через первые производные от перемещений по координатам. Эти первые производные должны быть непрерывны, следовательно, волны рассматриваемого типа не могут нести разрывов скоростей или разрывов напряжений. Для стержня мы сразу предположим, что на фронте волны скорость и деформация, а следовательно, напряжение, меняются скачком, и получим скорость фронта в этом предположении. Возможность распространения ударных волн в неограниченной упругой среде со скоростями с4 и с2 требует дополнительного обоснования. Для продольных волн сильного разрыва применение этого обоснования получается в результате буквального повторения анализа § 2.10 для стержня. Совершенно аналогичные рассуждения, основанные на теореме о количестве движения, позволяют установить возможность распространения ударных волн искажения. Таким образом, уравнения движения упругой среды допускают решения, содержащие разрывы первых производных от перемещений. [27]

Страницы: 1 2