Знание - дисперсия
Cтраница 1
Знание дисперсии и функции корреляции позволяет найти среднеквадратичное значение разности между величинами Qj ( z, А. [1]
 |
Определение вероятности выполнения комплекса работ. [2] |
Знание дисперсий позволяет оценить вероятность выполнения той или иной работы или всего комплекса работ в заданный срок. [3]
Знание дисперсии входа недостаточно для расчета дисперсии выходного сигнала. [4]
Знание дисперсии прибора еще недостаточно, чтобы сказать, можно ли будет наблюдать две соседние линии раздельно. В случае нечетких, размытых линий они сольются, в то время как в качественно выполненном и подготовленном приборе они будут видны раздельно, хотя дисперсия этого прибора может оказаться даже меньшей, чем у первого прибора. [5]
Однако знание дисперсии прогнозируемой величины отнюдь не характеризует полностью качества и надежности прогноза. Последняя определяется границами того интервала, внутри которого с заданной вероятностью она находится. Для определения указанного интервала необходимо знать или задаться плотностью вероятности прогнозируемой величины. [6]
Использование вышеприведенных процедур предполагает знание дисперсий а2 и ст2 ( / 1 - s - т); если это требование не выполняется, то точные значения дисперсий заменяются оценками. [7]
Это более сложный случай, поскольку для построения критериев необходимо знание дисперсий. Поэтому сравнение средних по эмпирическим данным производится в два этапа. [8]
Как видно из равенства ( 3), для оценки точности среднего результата необходимо знание дисперсии генеральной совокупности. Обычно дисперсия является неизвестней до опыта и о ней приходится судить на основании результатов измерения. [9]
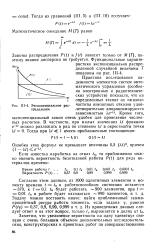 |
Экспоненциальное распределение. [10] |
Законы распределения P ( t) и / ( /) зависят только от М Т, поэтому знание дисперсии не требуется. [11]
В интегральных спектрах звездных систем ( шаровых звездных скоплений, центральных областей галактик и др.) ширина линий определяется дисперсией скоростей звезд вдоль луча зрения. Знание дисперсии скоростей в изолированных системах позволяет на основании вириала теоремы оценить массу систем ( А. [13]
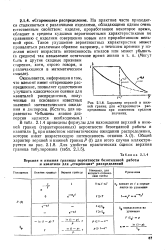 |
Характер верхней и нижней границ для стареющего распределения при известном среднем значении. [14] |
Оказывается, информация о том, что элемент имеет стареющее распределение, позволяет существенно улучшить классические оценки для квантилей распределения, полученные на основании известных значений математического ожидания и дисперсии. Кстати, для неравенства Чебышева знание дисперсии является необходимым. [15]
Страницы: 1 2
