Знание - среднее значение
Cтраница 1
Знание среднего значения еще не дает полной характеристики данного набора случайных величин. [1]
Знание среднего значения случайной величины и ширины кривой нормального распределения позволяет уверенно судить о возможном и невозможном. [2]
Однако знание только среднего значения случайной величины недостаточно для того, чтобы представить себе расположение значений случайной величины относительно ее среднего значения. [3]
Нельзя считать, что знание только средних значений может быть достаточным для решения подобной задачи; нельзя недооценивать важную роль стандартных отклонений. Искусственная модель, полученная нами, учитывает эти стандартные отклонения. [4]
Для такой сумматорной величины знание средних значений чисел заполнения позволяет непосредственно написать выражение для ее среднего значения. Если в дополнение к средним значениям чисел заполнения мы умеем найти и средние значения их попарных произведений, то это дает нам возможность непосредственно написать и дисперсию любой сумматорной величины. Всеми этими соображениями объясняется, почему в любом систематическом изложении квантовой статистики авторы считают своей важнейшей первоначальной целью отыскание именно средних значений чисел заполнения. [5]
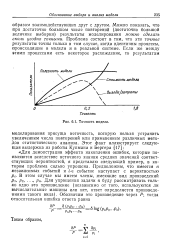 |
Точность модели. [6] |
Для демонстрации эффекта накопления ошибок, которые появляются вследствие неточного знания средних значений соответствующих вероятностей, я представлю следующий пример, в котором проблема сильно упрощена. [7]
Для конструирования знание разброса прочностных свойств почти так же необходимо, как знание среднего значения. Разброс усталостных свойств углепластиков требует дальнейшего изучения лучше всего с использованием материалов, изготовленных в условиях массового производства с хорошим контролем качества. [8]
Все статистические характеристики гауссовского процесса определяются функциями вероятности первого и второго порядков, так что знаний среднего значения и функции ковариа-ции достаточно для того, чтобы полностью установить все статистические свойства процесса. [9]
Часто Б гидравлике не требуется знать точную картину состояния движения каждой частицы жидкости, которая иногда может быть выявлена предыдущим методом. Достаточно бывает ограничиться знанием средних значений той или иной величины. [10]
Это позволяет, как показал Файлон, сделать важное обобщение задачи о плоском напряженном состоянии, приводящее в случае тонкой пластины к двумерной задаче. Основная идея Файлона состоит в том, что знание средних значений компонент тензора, напряжений и вектора перемещения по малой толщине пластины равноценно знанию их действительных значений в каждой точке. [11]
Проницаемость определяется при исследовании кернов, отбираемых при бурении продуктивного горизонта, а также по фактическим данным исследования скважин. Для гидродинамических расчетов по разработке нефтяных месторождений требуется знание среднего значения проницаемости пласта. Среднее значение проницаемости по кернам отдельных скважин установить практически невозможно. [12]
Эти жесткие и конкретные требования как раз и выражают принцип максимальной эффективности, который, в нашем случае, приводит к обязательному выполнению условий полноты исследований при оптимальной сети разведочных, добывающих и наблюдательных скважин. Однако на практике их соблюдение вступает в противоречие со стремлением к экономии затрат труда, времени и материальных ресурсов. В борьбе про -, тивоположных начал и вырабатывается представление об-оптимальной ( необходимой и достаточной для решения задач) полноте исследований при изучении геологического строения объекта. Кроме того, в технологических расчетах разработки требуется знание средних значений определяемых параметров и. В проводимом примере базовая методика Главтюменгеологии позволяет, интерпретировать в среднем до шести проплаетков. [13]
В любом случае речь идет о создании эквивалентной модели по отношению к реальному водоносному пласту. В этой связи полезно отметить следующее. Из структуры формулы ( 1) получается, что погрешность в знании среднего значения коэффициента пьезопроводности в некоторой мере ( так как х еще входит в параметр fo) компенсируется за счет определяемого параметра проводимости. [14]
При определении запасов прочности часто используют результаты экспериментальных исследований. Так как чпсло испытаний неизбежно огранп-нено, то возникает вопрос о возможных значениях измеряемого параметр. Например, требуется определить вероятность появления в лопатках турбомашин опасных переменных напряжений по данным тензометрирования 15 - 20 лопаток. Предполагаем, что закон распределения для рассматриваемой совокупности деталей является нормальным и тогда для расчета требуется знание среднего значения и среднего квадратичного отклонения. [15]
Страницы: 1