Знание - решение
Cтраница 1
Знание решения этой задачи требуется при анализе взаимод. [1]
 |
Устойчивые и неустойчивые предельные режимы угловой скорости ведущего вала вариатора. [2] |
Вместе с тем знание решения в и ( t) позволяет выделить области допустимых начальных условий, при которых возникают устойчивые и неустойчивые предельные режимы угловой скорости движения звена приведения машинного агрегата. [3]
Заметим, что знание решения задачи Римана может оказаться полезным и в других численных приложениях. В частности, использование решения задачи Римана, а также некоторых его элементов, может повысить надежность, устойчивость или точность того или иного метода. При этом если работа Monaghan ( 1997) позволила усовершенствовать вид искусственной вязкости, применяемой в данном методе, то применение линеаризованных формул распада произвольного разрыва в работе Паршикова ( 1999) позволило отказаться от применения искусственной вязкости. [4]
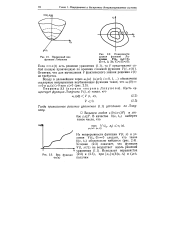 |
Примерный вид функции Ляпунова.| Поверхности уровня функции Ляпунова V ( xi, Xt C, ( 1, 2, 3. С С С3.| Вид функции. [5] |
Отметим, что для вычисления V фактического знания решения x ( t) не требуется. [6]
Этап выполняется только при инициализации системы диагностики и завершается ее отладкой - накоплением в базе знаний решений алгоритма в процессе тестового ситуационного обучения. [7]
Отсюда следует, что определение замены переменных, преобразующей первоначальное уравнение ( 1) в простейшее уравнение ( 8), предполагает знание решения первоначальной системы. Следовательно, нахождение решения уравнения Крылова - Боголюбова в этом случае эквивалентно нахождению решения исходной системы ( 1), поэтому решение задачи о преобразовании уравнений не стало более легким. [8]
Должно быть отмечено и теоретическое значение метода, так как с его помощью можно делать заключения о существовании, единственности и области расположения решения уравнения, не находя самого решения, что подчас не менее важно, чем фактическое знание решения. [9]
Нужные для вычисления величины 6j разрывов производных могут быть найдены последовательно, используя величины ранее вычисленных разрывов и значения решения на предыдущих шагах. Для линейных уравнений знание решения по требуется и величины разрывов могут быть определены независимо от самого процесса решения. [10]
Таким образом, из рядов в выражении (3.47) могут быть выделены в конечной форме медленно сходящиеся части; остающиеся после такого выделения ряды будут быстро сходиться. Заметим еще, что знание решения для произвольного распределения сосредоточенных сил позволяет составить решение, соответствующее нагрузке, распределенной по произвольному закону. Соответствующие суммы ( по / от 1 до N) должны быть при этом заменены интегралами. [11]
Но общих методов решения таких систем не существует. Поэтому для доведения решения задачи до конца желательно вводить малый параметр так, чтобы было известно не только периодическое, но и общее решение порождающей системы. В этом случае систему из п независимых частных решений уравнений в вариациях легко найти согласно теореме Пуанкаре путем дифференцирования по параметрам. Достаточным является и знание решения порождающей системы, зависящего ог п - 1 параметров, так как при наличии ( п - 1) - го независимого частного решения системы с периодическими коэффициентами еще одно решение можно определить с помощью квадратур. [12]
Но общих методов решения таких систем не существует. Поэтому для доведения решения задачи до конца желательно вводить малый параметр так, чтобы было известно не только периодическое, но и общее решение порождающей системы. В этом случае систему из п независимых частных решений уравнений в вариациях легко найти согласно теореме Пуанкаре путем дифференцирования по параметрам. Достаточным является и знание решения порождающей системы, зависящего ог п - 1 параметров, так как при наличии ( п - 1) - го независимого частного решения системы с периодическими коэффициентами еще одно решение можно определить с помощью квадратур. [13]
Страницы: 1