Двухкомпонентный раствор

Cтраница 3

Обычно коэффициент распределения / компонентов между двумя двухкомпонентными растворами определяют как отношение мольных долей компонентов в одном растворе, деленное на отношение мольных долей компонентов в другом равновесном растворе. [31]

В результате этого вытеснения на поверхности адсорбента образуется гомогенный поверхностный двухкомпонентный раствор. [32]

Измерение показателя преломления дает возможность непосредственно установить концентрацию двухкомпонентных растворов. Для этого используются эмпирические расчетные формулы и графики, так как теоретический расчет показателей преломления растворов с требуемой степенью точности в настоящее время еще невозможен. Сочетание рефрактометрических измерений с определением других физических свойств или с химической обработкой исследуемого вещества позволяет анализировать тройные и более сложные смеси и определять таким образом состав многих важных промышленных продуктов и биологических объектов. [34]

Типичная пограничная кривая двухкомпонентной смеси. [35]

Уравнение ( 10) описывает как кривую сосуществования двухкомпонентного раствора, так и пограничную кривую. Уравнение пограничной кривой определяет связь между давлением и температурой на линии, ограничивающей область двухфазных состояний при заданной средней концентрации. [36]

Изопиестические парциальные величины не имеют смысла в случае двухкомпонентного раствора соль - вода, поскольку изменение состава раствора здесь несовместимо с постоянством лш. [37]

Здесь и в последующем изложении в целях простоты рассматриваются только двухкомпонентные растворы. Обобщение на случай большего числа компонентов принципиальных трудностей не представляет. [38]

Для учета взаимодействия мигрантов при катионном обмене предлагается модель двухкомпонентного раствора [1, 17], основанная на предположении о независимости процесса ионного обмена для каждой пары ионов от содержания других ионов. [39]

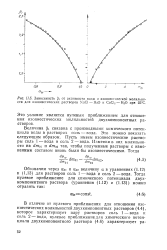Зависимость ( 5i от активности воды и изопиестической моляльно-сти для изопиестических растворов КаС1 - Н2О и СаС12 - HjO при 25ЭС. [40]

Это условие является нулевым приближением для отношения изопиестических моляльностеи двухкомпонентных растворов. [41]

Допустим, что приемлемо нулевое приближение для химических потенциалов двухкомпонентного раствора - условие (4.6) гл. [42]

Скривеном [65] получено также автомодельное решение, когда жидкость - двухкомпонентный раствор и рост пузырька зависит не только от теплопроводности, но и от диффузии испаряющейся компоненты в жидкости. В работе [57] проведено обобщение результатов [65 ] на случай роста пузырька в неоднородном температурном поле. Выведено соотношение, справедливое для двух режимов: 1) когда рост пузырька определяется силами инерции; 2) теплоотдачей. [43]

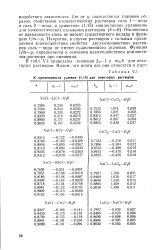К применимости условия для некоторых растворов. [44]

Напротив, в случае растворов с сильным проявлением взаимодействия свойства двухкомпонентных растворов соль - вода не имеют существенного значения. Функция 1 / т - z / i определяется в основном взаимодействием компонентов раствора при смешении. [45]

Страницы: 1 2 3 4