Знание - напряженное состояние
Cтраница 1
Знание напряженного состояния в прослойке позволяет определить величину сопротивления. [1]
Знание напряженного состояния в прослойке позволяет определить величину сопро-тиапения. [2]
Знание напряженного состояния горных пород и контроль за его изменением в процессе строительства гидротехнического сооружения и наполнения водохранилища дает возможность предвидеть деформации в основании плотины и своевременно принять меры для снижения или ликвидации нежелательных смещений. Для этой цели в скважинах большого диаметра ( до 1250 мм) и глубиной до 70 м устанавливают специальную контрольно-измерительную аппаратуру ( КИА), включающую комплекс различных приборов. [3]
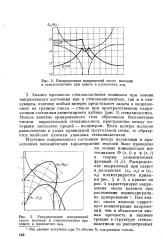 |
Распределение напряжений около волокон в стеклопластике при сдвиге в плоскостях.| Распределение напряжений около волокон в стеклопластике при сдвиге в плоскостях. [4] |
Анализ прочности стеклопластиков возможен при знании напряженного состояния как в стекдонаполнителе, так и в связующем, поэтому особый интерес представляет задача о напряжениях на границе смола - стекло при пространственном напряженном состоянии элементарного кубика ( рис. 1) стеклопластика. Модель линейно армированного тела образована бесконечным числом параллельных стекловолокон, пространство между которыми заполнено средой - полимером. Если центры волокон расположены в узлах правильной треугольной сетки, то образуется наиболее плотная упаковка стеклопластиков. [5]
При наличии в теле трещины для суждения о характере ее распространения и тем самым для суждения о прочности также необходимо знание напряженного состояния. Задача определения напряженного состояния около конца трещины отличается от обычных задач определения концентрации напряжений тем, что геометрически линеаризованная постановка краевых условий и физически линейная теория упругости приводят к бесконечным напряжениям и бесконечным градиентам напряжений в конце тонкого разреза. При этом понятие коэффициента концентрации напряжений теряет смысл. Разумеется, можно было бы пытаться сохранить числовое безразмерное выражение коэффициента концентрации напряжений посредством учета сложных детальных особенностей деформации материала у конца разреза. Однако для решения задач о трещине совсем не обязательно интересоваться детальными процессами, идущими в весьма малой окрестности конца разреза. [6]
При наличии в теле трещины для суждения о характере ее распространения и тем самым для суждения о прочности также необходимо знание напряженного состояния. Задача определения напряженного состояния около конца трещины отличается от обычных задач определения концентрации напряжений тем, что геометрически линеаризованная постановка краевых условий и физически линейная теория упругости приводят к бесконечным напряжениям и бесконечным градиентам напряжений в конце тонкого разреза. При этом понятие коэффициента концентрации напряжений теряет смысл. Разумеется, можно было бы пытаться сохранить числовое безразмерное выражение коэффициента концентрации напряжений посредством учета сложных детальных особенностей деформации материала у конца разреза. [7]
При наличии в теле трещины для суждения о характере ее распространения и тем самым для суждения о прочности также необходимо знание напряженного состояния. Задача определения напряженного состояния около конца трещины отличается от обычных задач определения концентрации напряжений тем, что геометрически линеаризованная постановка краевых условий и физически линейная теория упругости приводят к бесконечным напряжениям и бесконечным градиентам напряжений в конце топкого разреза. При этом понятие коэффициента концентрации напряжений теряет смысл. Разумеется, можно было бы пытаться сохранить числовое безразмерное выражение коэффициента концентрации напряжений посредством учета сложных детальных особенностей деформации материала у конца разреза. [8]
При наличии в теле трещины для суждения о характере ее распространения и тем самым для суждения о прочности также необходимо знание напряженного состояния. Задача определения напряженного состояния около конца трещины отличается от обычных задач определения концентрации напряжений тем, что геометрически линеаризованная, постановка краевых условий и физически линейная теория упругости приводят к бесконечным напряжениям и бесконечным градиентам напряжений в конце тонкого разреза. При этом понятие коэффициента концентрации напряжений теряет смысл. Разумеется, можно было бы пытаться сохранить числовое безразмерное выражение коэффициента концентрации напряжений посредством учета сложных детальных особенностей деформации материала у конца разреза. [9]
При наличии в теле трещины для суждения о характере ее распространения и тем самым для суждения о прочности также необходимо знание напряженного состояния. Задача определения напряженного состояния около конца трещины отличается от обычных задач определения концентрации напряжений тем, что геометрически линеаризованная постановка краевых условий и физически линейная теория упругости приводят к бесконечным напряжениям и бесконечным градиентам напряжений в конце тонкого разреза. При этом понятие коэффициента концентрации напряжений теряет смысл. Разумеется, можно было бы пытаться сохранить числовое безразмерное выражение коэффициента концентрации напряжений посредством учета сложных детальных особенностей деформации материала у конца разреза. [10]
 |
Основные виды деформации поверхности трещины. [11] |
При наличии в теле трещины для суждения о характере ее распространения и тем самым для суждения о хрупкой прочности также необходимо знание напряженного состояния. [12]
 |
Основные виды деформации поверхности трещины. [13] |
При наличии в теле трещины для суждения о характере ее распространения и тем самым для суждения о хрупкой прочности также необходимо знание напряженного состояния. [14]
В литературе опубликовано достаточно много работ, в которых использован ПОМ для исследования напряжений в эластичных деталях уплотнительных устройств общего назначения, а также теоретических исследований, показывающих, что знание напряженного состояния и численных значений возникающих напряжений позволяет рассчитать выносливость эластичных деталей и прогнозировать долговечность уплотнительных устройств. Применительно к уплотнениям буровых насосов выполнена лишь одна работа по исследованию качественной картины напряженного состояния резиновых манжет поршня [11] простейшей формы. [15]
Страницы: 1 2