Знание - функция - распределение
Cтраница 1
Знание функции распределения дает исчерпывающее представление о значениях появления интересующего нас признака. Поэтому результаты наблюдений массовых проявлений интересующих признаков стремятся сравнить с известными функциями распределений. Любое статистическое исследование вначале требует сбора и упорядочивания первичного статистического материала. В результате статистической группировки, предполагающей распределение наблюдаемых признаков на однородные группы, получают статистические ряды распределений, по которым уже можно рассчитать определенные параметры распределений. [1]
Знание функции распределения той или иной физической величины позволяет производить различные статистические подсчеты. [2]
Однако возможен и другой подход, основанный на знании функций распределения интервалов между моментами прибытия пользователей FI и функции распределения длительности разговора по телефону FZ. При этом моделирование фактически сводится к выработке значений вышеуказанных случайных величин и их логико-математической обработке для формирования числовых значений моментов наступления событий в системе и значений переменной, характеризующей размер очереди. Одновременно выполняются действия, обеспечивающие накопление статистики. [3]
Эти формулы показывают, что знание характеристической функции эквивалентно знанию функции распределения. [4]
Знание всех возможных моментов скоростей частиц, очевидно, эквивалентно знанию функции распределения. [5]
Как видно из уравнения (XVI.37), для вычисления абсолютных скоростей реакций необходимо знание функций распределения исходных веществ и переходного состояния, определенных методами статистической термодинамики на основе спектроскопических данных. Величина функции распределения для переходного состояния может быть найдена, если известна поверхность потенциальной энергии. [6]
В этих методах - предполагается, что априорная информация о системе сводится к знанию функции распределения времени безотказной работы F ( t) и иикакой другой информации о внутреннем состоянии системы, кроме сигнала об отказе, нет. В таком случае задача ТО сводится к определению возраста системы, после достижения которого проводится профилактика. [7]
Используемый здесь метод проверки гипотезы равенства дисперсий в двух генеральных совокупностях по независимым выборкам основан на знании функции распределения Фишера. Поэтому для получения значимых оценок необходимо в память ЭЦВМ ввести таблицу критических точек этого распределения. [8]
Следует отметить, что в случае каких-либо априорных сведений о поведении функции п ( х) в особой области знание функции распределения величины Vj j; позволяет построить более мощные критерии, чем х2 - кРитеРии - Например, если заведомо известно, что ц ( к) лежит по одну сторону от полученной регрессионной кривой, то, очевидно, можно построить односторонний критерий более мощный, чем х2 - критерий. [10]
Для задач, относящихся к классу статистических, применяются обучаемые методом проб и ошибок нейросети, являющиеся байесовскими классификаторами, работающими в условиях отсутствия знания функций распределения вероятностей. [11]
Если поле ероятностей ( Q, , Р) - борелевское, то значения вероятностной функции Р % ( А) для всех бо-релевских множеств А из И однозначно определяются знанием функции распределения F % ( x) ( ср. Так как главным образом интересуются только этими значениями Р % ( А), то функци t распределения играют во всем дальнейшем изложении существенную роль. [12]
Если поле ероятностей ( R, f, Р) - борелевское, то значения вероятностной функции Р % ( А) для всех бо-релевских множеств А из R однозначно определяются знанием функции распределения F ( x) ( ср. Так как главным образом интересуются только этими значениями Рь ( А), то функци t распределения играют во всем дальнейшем изложении существенную роль. [13]
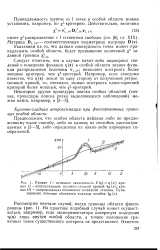
Рентгенографические и другие структурные исследования показали, что в жидкостях существует определенная степень упорядочения атомов, связанная с ближним порядком. Знание функций распределения, характеризующих структуру системы, и законов взаимодействия образующих ее частиц должно быть в принципе достаточным фундаментом для построения статистико-механической теории равновесных свойств системы взаимодействующих частиц. Если силы взаимодействия могут быть хорошо описаны на языке некоторых эффективных двухчастичных взаимных потенциалов, то полная потенциальная энергия системы для любой фиксированной конфигурации системы представляется функцией бинарного типа. [14]
Таким образом, характеристическая функция J) ( s) может быть разложена в ряд Тейлора по параметру s, причем коэффициентами этого разложения являются моменты случайной величины. Отсюда следует также, что знание всех моментов эквивалентно знанию функции распределения. [15]
Страницы: 1 2