Значение - средняя длина - свободный пробег
Cтраница 1
Значение средней длины свободного пробега используется, например, при описании диффузии, теплопроводности и других явлений. [1]
На рисунке приведены значения средней длины свободного пробега, определяемой эффективным сечением для передачи импульса. [2]
В табл. 4 приведены значения средней длины свободного пробега молекул воздуха при 0 д С и различных давлениях. [3]
Формула (42.12) в соответствии с опытом дает значения средней длины свободного пробега электрона, на два порядка превышающие период кристаллической решетки. [4]
В элементарной теории для всех молекул используется одно и то же значение средней длины свободного пробега молекул независимо от их скорости. В действительности среднее расстояние, проходимое молекулами между столкновениями, различно, если молекулы обладают не равными скоростями. [5]
Применение формул кинетической теории и теории переходных состояний приводит к нахождению маловероятных значений средней длины свободного пробега диффундирующей молекулы порядка нескольких сот ангстрем. Для получения физически оправданных значений длин свободного пробега Баррер17 предположил, что при элементарном акте диффузии энергия активации распределяется на большое число степеней свободы. [6]
Исходя из наблюдаемых на опыте значений удельной электропроводности ( или р I / Y), можно подсчитать, какие значения средней длины свободного пробега электрона X соответствуют опытным данным. Между тем в теории Друде - Лоренца считалось, что электрон имеет среднюю длину свободного пробега, сравнимую с расстояниями между ионами в кристаллической решетке металлов. [7]
Хотя статистическая взаимосвязь электронов, учитываемая принципом Паули, и не должна приниматься во внимание в явной форме, тем не менее может создаться впечатление, что она должна содержаться в неявном виде в значении средней длины свободного пробега. Бриллюен отметил, что последнее должно превышать то значение длины свободного пробега / о, которое мы получили бы без учета статистической взаимосвязи электронов. [8]
В заключение отметим, что распределение по длинам свободных пробегов (44.6), как и распределения Максвелла, не имеет ограничений со стороны больших плотностей и может быть применимо для плотных газов. Распределение зависит от величины / и, которая является функцией плотности среды. Значение 1Я легче всего определяется из (44.8) по значению средней длины свободного пробега. [9]
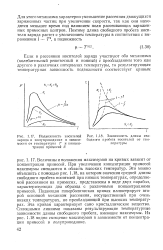 |
Подвижность носителей заряда п полупроводнике в зависимости от температуры Т и концентрации примесей N.| Зависимость длины свободного пробега носителей от температуры. [10] |
При увеличении концентрации примесей максимумы смещаются в область высоких температур. Это можно объяснить с помощью рис. 1.18, на котором значения средней длины свободного пробега носителей при низких температурах, определяемой рассеянием на примесях, представлены в виде двух парабол, характеризующих два образца с различными концентрациями примесей. Падающая гиперболическая кривая иллюстрирует второй основной механизм рассеяния, несущественный при очень низких температурах, но преобладающий при высоких температурах. Эта кривая характеризует само кристаллическое вещество. Сплошными линиями показаны результирующие температурные зависимости длины свободного пробега, имеющие максимумы. Из рис. 1.18 видно смещение максимумов в зависимости от концентрации примесей в полупроводнике. [11]
При использовании источников ультрафиолетового излучения необходимо помнить о слабых линиях, которые, как правило, сопровождают основное излучение. Пренебрежение возможностью влияния этих относительно слабых линий может привести к неправильной интерпретации спектров УФЭ. Значение глубины выхода фотоэлектронов в методе УФЭС изменяется в широких пределах от нескольких единиц до нескольких десятков ангстрем. Отметим, что имеются экспериментальные сложности в определении значения средней длины свободного пробега фотоэлектронов таких низких энергий, обусловленные, в частности, состоянием поверхности исследуемого материала, которое, по-видимому, приводило к завышенным значениям, полученным в ранних работах. [12]
Страницы: 1