Растяжение - пластина
Cтраница 3
Рассуждениями, аналогичными проведенным в § 8.2, можно показать, что функции и и v описывают растяжение пластины, а функции J, У. [31]
При растяжении пластин с двумя симметричными выточками ( см. рис. 10, а), как и при растяжении пластин с отверстием, происходит смещение максимума осевых растягивающих напряжений от дна выточки в тело пластины. [32]
Если температурное поле не вызывает значительных усилий в срединной плоскости пластины, то в уравнении (5.3.2) можно не учитывать влияния растяжения пластины на ее изгиб. [33]
Помимо испытаний образцов на изгиб, для определения предельного состояния по прочности и сопротивления хрупкому разрушению производятся также описанные ниже испытания на растяжения пластин большой ширины. Можно считать, что при испытании на изгиб легче получить хрупкое разрушение, так как наличие градиента номинального напряжения ограничивает возможность поперечного сужения и таким образом создает двустороннее растяжение посередине ширины образца. [34]
Градиент GJ характеризует скорость падения напряжений в плоскости хОг около точки О, Выражение для этого градиента можно принять таким же, как при растяжении пластины в боковыми надрезами. [35]
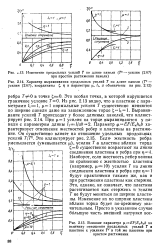 |
Характер выравнивания продольных усилий Т по длине панели ( Т - усилия, координаты., т и параметры ц, It, а обозначены иа.| Влияние параметра iEF / Exhxb на. [36] |
Наоборот, если жесткость ребер велика по сравнению с жесткостью пластины ( например, ц10) усилия Т на линии соединения пластины и ребра при г будут практически такими же, как и при растяжении пластины как стержня. Это, однако, не означает, что пластина растягивается как стержень и УСИЛИЯ Г не будут меняться по ширине пластины. [37]
В качестве примера в табл. 3.1 представлены данные [1] для клеевых соединений алюминиевого сплава и стали на малоусадочных модифицированных наполненных эпоксидных клеях для двух способов испытаний на сдвиг: кручение склеенных встык труб и сдвиг при растяжении пластин, склеенных внахлестку. Там же представлены когезионные свойства клеев. [38]
Докритическпй рост продольной сквозной трещины в длинной цилиндрической трубке из вязко-упругого материала под действием внутреннего давления р определим в соответствии с уравнениями (37.17), принимая коэффициент интенсивности напряжений в виде (29.25), а в качестве реологической модели, так же как п в задаче о растяжении пластины - тело Кельвина. [40]
Докритический рост продольной сквозной трещины в длинной цилиндрической трубке из вязкоупругого материала под действием внутреннего давления р определим в соответствии с уравнениями (5.21), принимая коэффициент интенсивности напряжений в виде (3.51), а в качестве реологической модели, так же как и в задаче о растяжении пластины, - тело Кельвина. [41]
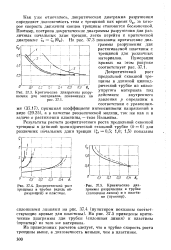 |
Критические диаграммы разрушения для материалов, показанных па.| Докритпческий рост трещины в трубке ( вдоль образующей и пластине. [42] |
Докритический рост продольной сквозной трещины в длинной цилиндрической трубке из вязко-упругого материала под действием внутреннего давления р определим в соответствии с уравнениями (37.17), принимая коэффициент интенсивности напряжений в виде (29.25), а в качестве реологической модели, так ке как н в задаче о растяжении пластины - тело Кельвина. [43]
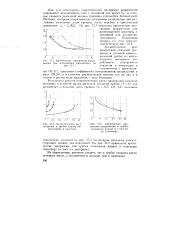 |
Критические диаграммы разру-материалов, показанных на.| Критические диаграммы разрушения в трубко ( (. плотная линия и в пластине ( пунктир.| Докрнтп гоский рост. [44] |
Докритическш с рост продольной сквозной трещины в длинной цилиндрической трубке из вязко-упругого материала под действием внутреннего давления р определим в соответствии с уравнениями (37.17), принимая коэффициент интенсивности напряжений в виде (29.25), а в качестве реологической модели, так же как и в задаче о растяжении пластины - тело Кельвина. [45]
Страницы: 1 2 3 4 5