Значение - резонансный интеграл
Cтраница 1
Значение резонансного интеграла ( 3 для этих случаев электронного возбуждения, найденное из уравнения ( 22), равно 17000 см-1. Возможно, что ароматические кольца диметиланилина и N-гетероароматического катиона образуют комплекс, в котором их ядра расположены в параллельных плоскостях. [1]
Очевидно, что значение резонансного интеграла & / становится небольшим, когда атомы i и / удалены один от другого на большое расстояние. Поэтому, если i и / - не соседние атомы, Хюккель такие интегралы приравнял нулю, а интегралы 3 / /, когда i и j - соседние атомы, принял равными друг другу и обозначил через р О последнем допущении можно заметить то же, что было сказано выше относительно кулоновского интеграла а. Хюккель отбросил также все интегралы перекрывания 5 7 ( i j j), что, однако, не вполне допустимо, потому что, как было показано позднее ( стр. В этом смысле допустимо отбрасывание интегралов 1 S / /, если только i и j - не соседние атомы. [2]
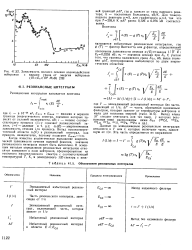 |
Зависимость полного сечения взаимодействия.| Обозначения резонансных интегралов. [3] |
Когда известно аналитическое выражение энергетической зависимости сечения ядерной реакции, значение резонансного интеграла может быть вычислено. [4]
 |
Х-5. Схема возмущения первого порядка при взаимодействии орбиталей с равными энергиями ( а и возмущение второго порядка при взаимодействии орбиталей, сильно различающихся по энергии ( б. [5] |
Взаимодействием молекулярных орбиталей у остальных атомов мы можем пренебречь, так как там орбитали практически не перекрываются и значение резонансного интеграла р близко к нулю. [6]
В ароматических полисульфидах положение энергетических уровней молекулы и в основном, и в возбужденном состоянии должно определяться 2п оптическими электронами атомов серы и т: - электронами бензольных колец. При расчете значения резонансного интеграла связи С-S и ку-лоновского интеграла атома серы были взяты такими же, как и для дифенилсульфида. Резонансный интеграл связи S-S выбирался равным 0 8jl На рисунке представлена схема энергетических уровней ряда рассчитанных полисульфидов. Наиболее длинноволновая полоса поглощения обусловлена переходом электрона с последнего заполненного молекулярного уровня на возбужденный уровень бензольного кольца. Увеличение числа атомов серы в цепочке приводит к повышению последнего заполненного уровня и, следовательно, к смещению полосы поглощения в более длинноволновую область спектра. Число возможных электронных переходов с энергией 1 - т - 2 Р растет с числом п, что должно приводить к наложению полос поглощения. Поэтому в области 200 - 400 ммк отмечается почти сплошной спектр поглощения полисульфидов с очень слабо выраженными максимумами. [7]
В ароматических полисульфидах положение энергетических уровней молекулы и в основном, и в возбужденном состоянии должно определяться 2п оптическими электронами атомов серы и я-электронами бензольных колец. При расчете значения резонансного интеграла связи С-S и ку-лоновского интеграла атома серы были взяты такими же, как и для дифенил сульфида. На рисунке представлена схема энергетических уровней ряда рассчитанных полисульфидов. Наиболее длинноволновая полоса поглощения обусловлена, переходом электрона с последнего заполненного молекулярного уровня на возбужденный уровень бензольного кольца. Увеличение числа атомов серы в цепочке приводит к повышению последнего заполненного уровня и, следовательно к смещению полосы поглощения в более длинноволновую область спектра. Число возможных электронных переходов с энергией 1 - - 2 р растет с числом п, что должно приводить к наложению полос поглощения. Поэтому в области 200 - - - 400 ммк отмечается почти сплошной спектр поглощения полисульфидов с очень слабо выраженными максимумами. [8]
Аналогичная ситуация наблюдается для всех углеводородов, не говоря уже о гетерсатомных молекулах. Причина такого несовпадения кроется, в том, что для описания энергий образования не подходит значение резонансного интеграла, полученное из соответствия со спектральными данными. При помощи одного значения резонансного интеграла р нельзя удовлетворительно описать свойства основного и возбужденных состояний. [9]
В расчетах использованы значения 1 - - - 14 49 эв, YNN 12 91 эв. Так же как в работе [11], в которой проведен расчет пиридина, для анионов значения резонансных интегралов приняты равными рсг - - 2 388 эв, л - - - - 2 576 эв. [10]
Если для параметра б выбрать другое значение, более точно отражающее электроотрицательность атома хлора, результат расчета заметно улучшится. Можно ожидать еще лучшего согласия между теорией и экспериментом, если принять во внимание интегралы перекрывания 5с - си5с - сь а также различие между значениями резонансных интегралов Рс-с и Рс - сь Такой расчет, выполненный для хлорбензола Хоу и Гольдштей-ном [7], и привел к значению цмез, равному 0 67 D. К сожалению, во многих случаях результаты даже наиболее совершенных расчетов плохо согласуются с экспериментальными значениями. [11]
Мы переходим к рассмотрению группы методов, позволяющих получать величины, которые можно считать приближениями к результатам метода МОХ. Будем искать решение для системы, которая мало отличается от исходной; пусть, например, новая система отличается значением кулоновского интеграла в положении ц либо значением резонансного интеграла связи ра. [12]
Аналогичная ситуация наблюдается для всех углеводородов, не говоря уже о гетерсатомных молекулах. Причина такого несовпадения кроется, в том, что для описания энергий образования не подходит значение резонансного интеграла, полученное из соответствия со спектральными данными. При помощи одного значения резонансного интеграла р нельзя удовлетворительно описать свойства основного и возбужденных состояний. [13]
В третьей, четвертой и пятой колонках табл. 7 приведены значения теоретической энергии резонанса трех типов. Символом J обозначен обменный интеграл. В четвертой колонке приведены значения резонансного интеграла р, определенные методом ЛКАО - МО. Значения у, приведенные в пятой колонке, требуют дополнительного объяснения. [14]
Величина резонансного интеграла, определяющего энергию и частоту резонанса, зависит от характера участвующих структур. В бензоле он велик ( около 36 ккал / мол); но может быть и гораздо меньше. Рассмотрим, какова была бы молекула бензола, если бы значение резонансного интеграла было очень мало, так что частота резонанса была бы меньше частоты колебания ядер. При любой конфигурации ядер в молекуле в большей или меньшей степени имеет место резонанс структур Кекуле. [15]
Страницы: 1 2