Значение - средний квадрат
Cтраница 1
Значения средних квадратов Н и Ну равны. [1]
Значения среднего квадрата, соответствующие различным длинным подвыборкам, часто имеют различный порядок величины. [2]
Значение среднего квадрата флуктуации заряда получают на основе простой операции. Снова рассмотрим одномерную модель резистора, описанную в разд. [3]
Это позволяет определить возрастание значения среднего квадрата ошибки слежения и среднего значения квадрата входной переменной, положив r ( t ] и vm ( t) равными нулю. [4]
Третий выходной параметр distor содержит значение среднего квадрата ошибки квантования. [5]
В результате совместного решения уравнений (5.196), (5.198) и (5.199) находятся значения среднего квадрата ошибки а, постоянной составляющей г, амплитуды А и частоты автоколебаний со. [6]
Если считать, что со находится значительно ниже наблюдаемого диапазона частот, то автокорреляционная функция и значение среднего квадрата x ( t) будут зависеть от времени измерения Т, как это обсуждалось в разд. С теоретической точки зрения представляет интерес проанализировать изменение этих статистических характеристик в пределе при Т - - оо. [7]
Следует заметить, что окончательное значение сумм квадратов по скорректированным данным, которые используются для получения значений средних квадратов, не дают при сложении общей суммы квадратов. Это характерно для неортогональных планов. [8]
Из уравнений (6.5) и (6.8) видно, что для определенной полосы частот с coi0 автокорреляционная функция и значение среднего квадрата процесса, спектральная плотность которого задается уравнением (6.3), сходятся в пределе к выражениям одного вида. Таким образом, 1 / / - шум в ограниченной полосе частот является по крайней мере стационарным процессом в широком смысле. [9]
Для модели I проверка существенности основных эффектов и эффектов взаимодействия осуществляется сравнением значений соответствующих им средних квадратов с значением среднего квадрата ошибки. [10]
Заметим, что автокорреляционная функция - четная функция временной задержки t и что ее значение при т 0 есть значение среднего квадрата процесса. [11]
Из этих выражений видно, что, отфильтровывая высокочастотную энергию входного сигнала, детектор увеличивает время корреляции в Тт / т раз и уменьшает значение среднего квадрата в обратное число т / тт раз. [12]
Поскольку искажение, которое связывает состояния, является осциллирующим, то, хотя среднее значение ф может, например, быть нулем, когда положение равновесия находится в 0, физический смысл будет иметь значение среднего квадрата, которое не будет равно нулю. В приведенном выше объяснении спектра при высоких температурах наблюдаемые значения g - факторов и других констант были средними по времени, так как частота колебаний ( в этом случае нулевых колебаний) велика по сравнению с частотой электронного спинового резонанса. [13]
Экспоненциальный вид этого выражения характерен для процесса релаксации. Значение среднего квадрата, получаемое из выражения (2.60), есть величина kQR / ti, которая становится бесконечно большой, если время релаксации становится бесконечно малым. В этом приближении тепловой шум является импульсным процессом. [14]
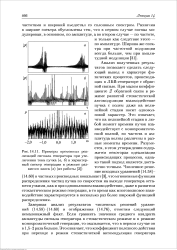 |
Примеры временных реализаций сигнала генератора при увеличении тока пучка ( а, б и характерный спектр генерации в режиме развитого хаоса ( в ( из работы. [15] |
Страницы: 1 2