Значение - квантиль
Cтраница 2
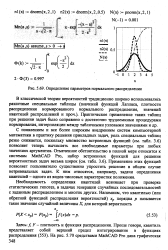 |
Определение параметров нормального распределения. [16] |
В классической теории вероятностей традиционно широко использовались различные специальные таблицы ( значений функций Лапласа, плотности распределения нормированного нормального распределения, значений квантилей распределений и проч. [17]
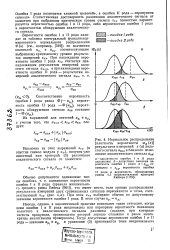 |
Нормальное распределение [ плотность вероятности wa ( x ] результатов измерений х ( а холостого сигнала аХол и близкого по величине аналитического сигнала аан. [18] |
Вероятности ошибок I и II рода находят из таблицы интегральной функции нормированного нормального распределения Ф ( и) ( см., например, [549]) по значениям квантилей upt и ир. [19]
Как видно из табл. 4.2, точность оценки неоднородности структуры исходного материала по статистическим параметрам распред-ления величин I и Н зависит от уровня нагрузки на индентор и значения квантиля нормального распределения. Для более высоких квантилей ошибка увеличивается. [20]
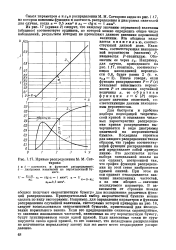 |
Кривые распределения М. М. Саттарова. [21] |
Иначе говоря, если функция распределения Р F ( х) указывает зависимость вероятности Р от значения случайной величины х, то обратная функция х G ( Р) определяет значения квантилей, соответствующие данным накопленным вероятностям. [22]
Пороговый уровень 8П в [89] ( проверка определителя) предлагалось безосновательно задавать в численным виде Sn 0 001, в [59] ( проверка определителя) и [84] ( проверка Е - и J-статистик) находить из таблицы % 2 -распределения по задаваемым значению квантиля и соответствующему количеству степеней свободы, а также вычислять по формульным выражениям. [23]
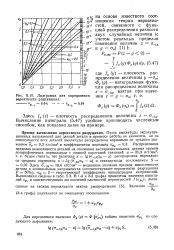 |
Диаграмма для определения НИИ Z у Оа, Т. е. [24] |
Вычисления сведены в табл. 5.3. В 1 - й и 2 - й графах приведены значения квантилей ир. [25]
Из смысла функции распределения следует, что каждому значению переменной величины ( абсциссе) соответствует значение функции ( ордината), по которой можно определить общее число ( долю) наблюдений, результаты которых не превышают данного значения переменной величины. Эта абсцисса называется квантилью, соответствующей данной доле. Квантиль, соответствующая накопленной вероятности ( частости) р, называется р-кван-тилью. Иначе говоря, если функция распределения рР ( х) указывает зависимость вероятности р от значения случайной величины х, то обратная функция xG ( p) определяет значения квантилей, соответствующие данным накопленным вероятностям. [26]
Страницы: 1 2