Значение - аргумент
Cтраница 1
Значения аргумента, при которых производная обращается в нуль или терпит разрыв, называются критическими точками или критическими значениями. [1]
Значение аргументов набирается тумблерным регистром. Значение истинности функции контролируется с помощью индикаторной лампочки. [2]
Значения аргумента и функции должны иметь десятичное основание с фиксированной точкой и двумя цифрами после запятой. Таким образом, тип получаемых значений функции должен быть явно описан. [3]
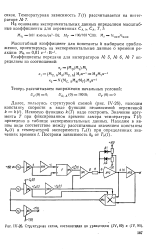 |
Структурная схема, составлевдая по уравцеццям ( J и ( IV, 90. [4] |
Значение аргумента Т при фиксированном времени замера температуры T ( t) приведено в таблице экспериментальных данных. [5]
Значения аргументов, определяющих допустимые значения погрешности Дд и ее составляющих, должны выбираться с учетом тех значений & t и ее составляющих ( особенно Да), которые будут характерны для периода использования данного СО, в том числе в результате его использования. [6]
Значения аргумента ш, при которых функция Jre ( w) обращается в нуль, называются корнями функции. Бесселя, корнем которой является wmn. Функция Jra ( w) многократно обращается в нуль. [7]
Значения аргументов представлены в левом верхнем углу табл. 5.1. Под ними расположены обозначения и значения логических функций, причем значения функций при конкретных наборах аргументов равны соответствующим разрядам их номеров, представленных двоичными кодами. [8]
Значения аргументов х и соответствующие им значения функции ft ( x) берут непосредственно из графика зависимости этих величин. [9]
Значение аргумента, при котором функция имеет наибольшую величину, называется точкой максимума. [10]
Значение аргумента, при котором функция имеет наименьшую величину, называется точкой минимума. [11]
Значения аргументов вводятся с перфокарт, функция М вычисляется по подпрограмме, которая выполняет также проверку аргументов на корректность. [12]
Значения аргумента х 2 и л; 3 обращают знаменатель дроби в нуль. [13]
Значения аргумента, при которых cos x 0, не являются решениями этого уравнения, так как если cos х - 0, то должно выполняться равенство 3 sin2 х О, а косинус и синус не могут быть одновременно равными нулю. [14]
Значения аргумента, при которых cos 0, не являются решениями этого уравнения, так как если cos x - Q, то должно выполняться равенство 2sm2x Q, но косинус и синус не могут быть одновременно равны нулю. [15]
Страницы: 1 2 3 4