Расчет - диск
Cтраница 2
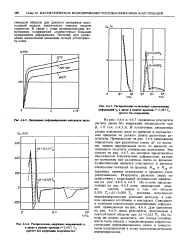 |
Диаграммы деформирования материала диска.| Распределение окружных напряжений в диске в момент времени / 2 083 7Ц ( расчет без коррекция погрешности.| Распределение остаточных пластических. [16] |
Результаты расчетов диска по уравнениям с коррекцией погрешности приведены на рис. 4.6.8 и 4.6.9. На основе представленных на рис. 4.6.8 эпюр напряжений можно сделать вывод о том, что области 0 005 ГЦД. Совпадают и значения накопленных пластических деформаций, приведенных на рис. 4.6.9. Для сравнения на рис. 4.6.9. даны результаты, полученные в неустойчивой области при Л 0 025 Тц. На основе их можно заключить, что потеря устойчивости счета связана с неравномерным упругопла-стическим деформированием диска и накоплением погрешностей в зонах упругопластического деформирования. [17]
Для расчета дисков на растяжение можно использовать малые и средние ЭВМ. [18]
Программа расчета диска на совместное действие растяжения и изгиба, приведенная в приложении 2 к гл. Программа позволяет рассчитывать диски на растяжение и изгиб с учетом действия растягивающих сил на изгиб в упругой и упругопластической области. [19]
Процедура расчета диска на ползучесть по теории старения не отличается от упругопластического расчета методом переменных параметров упругости. В первом приближении проводят расчет в упругой области, находят at в каждой точке диска, по изохронным кривым ползучести определяют секущий модуль Ecl) - / ( ог 0)) первого приближения для каждой точки и fj ( 1) и далее проводят обычную процедуру метода переменных параметров, описанную выше. [20]
Для расчета упруго-пластического диска должны быть заданы схема разбивки на участки и размеры диска, число его оборотов, величина напряжений на внешнем и внутреннем радиусах ага и an -, материал, закон изменения по радиусу температуры, модуль упругости, коэффициент линейного расширения и, наконец, кривые деформирования материала диска в диапазоне температур в диске. Эти кривые приведены в специальных справочных руководствах. [21]
Для расчета диска постоянной толщины проводятся следующие построения. [22]
Для расчета дисков переменной толщины по методу начальных параметров с применением ЭЦВМ исходные уравнения деформаций (2.4), (2.5), упругости (3.3), (3.4) и равновесия (3.7) целесообразно привести к двум дифференциальным уравнениям первого порядка с двумя неизвестными. [23]
Для расчета диска постоянной толщины проводятся следующие построения. [24]
Для расчета дисков более сложных профилей, где решение в замкнутой форме найдено быть не может, применяются приближенные методы. [25]
При расчете диска следует принимать число сечений более шести, располагая их ближе друг к другу в местах более резкого изменения толщины диска. [26]
При расчете дисков, толщина которых меняется значительнее, а отношение а мало, формулы ( 3 - 25) следует использовать в сочетании с приведенным в § 3 - 4 методом расчета ряда деталей, соединенных между собой по кольцевым поверхностям посредством напряженной посадки. [27]
 |
Транспортирующий диск машины ПП-600-И. [28] |
При расчете дисков определяют напряжения и деформации в опасных сечениях диска; кроме того находят первую, а при необходимости и вторую критические скорости. [29]
При расчете диска без отверстия для вала этот метод отличается от описанного выше лишь тем, что тангенциальное и радиальное напряжения на внутреннем ( нулевом) радиусе первого участка берут равными один другому: одно произвольное значение для первого расчета, второе произвольное значение для второго расчета. [30]
Страницы: 1 2 3 4