Расчет - живучесть
Cтраница 1
Расчет живучести на стадии проектирования сложных металлоконструкций типа статически неопределимых рам транспортных машин и другой подобной техники носит ориентировочный приближенный характер. Это связано с тем, что расчетным путем затруднительно выявить момент перехода материала конструкции из стадии накопления собственно усталостных повреждений в стадию роста усталостных трещин, тогда как каждая из этих стадий разрушения хорошо прогнозируется. Кроме того, расчетным путем трудно выявить отдельный элемент сложной металлоконструкции, в котором зарождается первая усталостная трещина, а также спрогнозировать порядок появления трещин в других элементах этой конструкции с - учетом влияния вновь появившихся трещин на кинетику трещин, возникших ранее. [1]
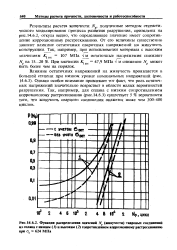 |
Функция распределения значений Nf ( живучести тавровых соединений из сплава с низким ( / и высоким ( 2 сопротивлением коррозионному растрескиванию при 0в 624 МПа. [2] |
Результаты расчета живучести Np, полученные методом статистического моделирования процесса развития разрушения, приведены на рис. 14.6.2, откуда видно, что определяющее значение имеет сопротивление коррозионному растрескиванию. От его величины существенно зависит влияние остаточных сварочных напряжений на живучесть конструкции. [3]
 |
Зависимость коэффициента х от отношения. [4] |
Приведенная методика расчета живучести конструкций основана на предположении, что кривые усталости ( см. рис. 19.1), полученные при испытаниях с постоянной амплитудой напряжений, отражают прочностные возможности конструкций и при переменных уровнях амплитуд напряжений. [5]
Таким образом, задача расчета живучести при случайных процессах нагружения сложной структуры может быть доведена до численных результатов. [6]
Таким образом, задача расчета живучести сводится к определению функции распределения коэффициента интенсивности для любого момента времени. [7]
Воспользуемся указанным экспериментальным фактом при расчете живучести пластины, нагруженной так, как показано на рис. 22.1. Поскольку скорость роста трещины пропорциональна частоте процесса нагружения и действующим напряжениям, то направление развития трещины будет определяться из условия максимума произведения этих величин. [8]
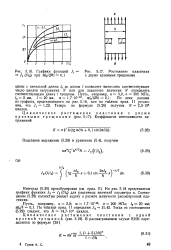 |
Графики функций при я / / ( 2 / 1 0 1. [9] |
Соотношение (5.29) полностью решает задачу о расчете живучести рассмотренной пластинки. [10]
Очевидно, что механика разруйхения должна стать базой для расчета живучести всех сложных технических объектов ( гл. Однако неясным остается вопрос, каким образом можно оценить ее долговечность до появления начальных трещин, не соответствующих классической механике разрушения. Этот вопрос имеет первостепенное значение, поскольку эксплуатация объектов с трещинами - это нарушение гарантий их безопасности для пассажиров. [11]
Из соотношений (20.1) - (20.3) следует, что задача расчета живучести сводится к определению функции распределения КИН для любого момента времени. [12]
Вместе с тем в ряде случаев при обосновании надежности возникает необходимость расчета живучести конструкций на стадии развития трещин. Учитывая, что начальные трещины статического и циклического эксплуатационного нагружения возникают в зонах повышенных местных уп-ругопластических деформаций, такой расчет должен основываться на предварительном исследовании закономерностей развития трещин как заведомо нелинейного процесса. В настоящее время практически отсутствуют решения задач нелинейной механики циклического нагружения для тех случаев, когда размеры зон циклических пластических деформаций превышают размеры трещин и действуют экстремальные эксплуатационные нагрузки. [13]
Из приведенных данных следует, что учет порогового значения КИН может значительно повысить точность расчета живучести конструкций. [14]
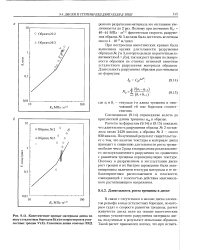 |
Кинетические кривые материала диска по шагу усталостных бороздок 8 ( я и скорости роста усталостных трещин V ( б. Сплошная линия отвечает ЕКД. [15] |
Страницы: 1 2