Расчет - модель
Cтраница 1
Расчет модели выполнен на базе статистических и расчетных величин за 1966 - 1985 гг. по основным отраслям, формирующим газовый комплекс. [1]
Расчеты модели из двух электронов и других моделей показывают, что средняя энергия взаимодействия электронов существенно зависит от числа полярных состояний, так как именно такие состояния дают наибольшие вклады в эту энергию. В следующих двух параграфах будут рассмотрены основные результаты, полученные при изучении этих моделей. [3]
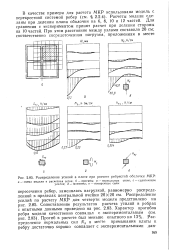 |
Распределение усилий в плите при расчете ребристой оболочки МКР. [4] |
Расчеты модели сделаны при делении плана оболочки на 6, 8, 10 и 12 частей. Для сравнения с экспериментом принят расчет при делении стороны на 10 частей. [5]
Расчет модели производится поэтапно. Если какой-либо работе предшествует несколько работ ( при связях типа FS), то дата ее начала принимается по максимальной величине даты раннего окончания всех предшествующих работ с учетом запаздывания или упреждения. Позднее начало и окончание работ рассчитываются аналогично, но в обратном порядке - от даты окончания последней работы к первой. Общий резерв времени ( total slack) - разница между датами позднего и раннего начала у первой и последней работы должен быть равен нулю. [6]
Расчет модели с многократным разветвлением слоев - см. Ландау Л.Д. II ЖЭТФ. [7]
 |
Газли-шые модели нагружепия для расчета вала и шарика шарикоподшипника. [8] |
Расчет модели более низкого уровня ( см. рис. 1.18, б) дает общее напряженное состояние, которое используется для оценки напряжений на сопрягаемых границах пространственного тела. Модели формы и их синтез имеют существенное значение для автоматизированного проектирования и конструирования. [9]
Расчету модели должно предшествовать изучение конструктивных особенностей моделируемого агрегата для выяснения возможностей упрощения модели без заметного искажения результатов исследования. Модель аппарата не макет: в ней должны быть воспроизведены лишь те конструктивные элементы, которые оказывают существенное влияние на изучаемый процесс. [10]
Дается расчет модели тела, предложенного Н. Е. Жуковским [1], удовлетворяющего условиям Гесса. [11]
Проведен расчет модели кристалла, поверхность которого полностью занята хемосорбатом, и показано, что эффективная масса электронов в зоне энергий, образующейся при гомеополярной хемосорбции, сравнима с эффективной массой электрона в зоне проводимости кристалла. При заполнении такой хемосорбционной зоны электронами из адсорбированных атомов или из кристалла может значительно изменяться поверхностная проводимость. [12]
Метод расчета модели и обработки опытных данных состоит в следующем. [13]
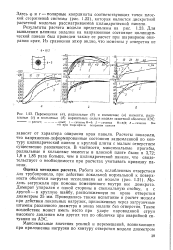 |
Перемещения ( а, радиальные ( б и кольцевые ( в моменты, радиальные ( г и кольцевые ( д нормальные силы в модели защитной оболочки АЭС. [14] |
Результаты расчета модели представлены на рис. 1.23. Для выявления влияния заделки на напряженное состояние цилиндрической панели был проведен также ее расчет при шарнирном опи-рании края. [15]
Страницы: 1 2 3 4
