Расчет - моноопора
Cтраница 1
Расчет моноопор для бурения на акваториях с глубинами до 10 м не представляет особого практического интереса. Изгибающий момент от волнового давления и продольных сил с уменьшением глубины моря и, следовательно, высоты моноопоры уменьшается. Поэтому на глубине до 10 м моноопора из обсадных труб даже с относительно малым внешним диаметром 0 168 м заведомо обладает достаточной прочностью. [1]
В дальнейшем при расчете моноопоры по схеме I рассматривается контакт моноопоры только с дальней стенкой проема. Высота стенки проема составляет менее 0 2 м, поэтому можно считать, что контакт моноопоры с проемом плавоснования имеет точечный характер и после его достижения изгибающий момент от качки плавоснования моноопоре не передается. [2]
Поэтому на практике при расчете моноопор более целесообразно использовать дифференциальный метод выбора коэффициентов запаса. В нем возможность отклонения в неблагоприятную сторону влияющих на напряженное состояние факторов учитывают путем введения коэффициентов запаса по каждому из них отдельно. [3]
Представляется, что при расчете моноопор все-таки необходимо учитывать податливость верхних слоев грунта морского дна, состоящих в большинстве случаев из илистых грунтов. Для этого целесообразно за расчетную высоту L моноопоры при описании условий закрепления ее нижнего конца моделью жесткой заделки принимать сумму высоты возвышения моноопоры над фактическим дном моря и 1 / 3 длины / участка, заглубленного в грунт. Здесь и далее под высотой моноопоры понимается ее расчетная высота, а под расчетным уровнем дна моря - уровень, лежащий на расстоянии 1 / 3 ниже фактического дна. [4]
Таким образом, если при расчете моноопоры оказывается, что ее частота близка нулю или устремляется в бесконечность, то это свидетельствует о близости режимов эксплуатации, в которых моноопорное основание способно потерять устойчивость. Проектирование моноопор на работу в этих условиях недопустимо. [5]
Этот метод приближенного решения также применим к расчету ступенчатых моноопор с постоянным по длине каждой отдельной ступени моментом инерции. Значение силы Р2 для ступенчатых моноопор следует выбирать, усредняя распределенную силу тяжести моноопоры по ее высоте. Упругая линия каждой ступени описывается в этом случае отдельным дифференциальным уравнением. Интегралы этих уравнений ( функции-решения у) выражаются через начальные параметры рассматриваемой ступени. [6]
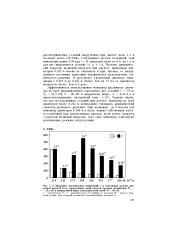 |
Диаграмма максимальных напряжений о в моноопорах разных диаметров высотой 18 м, нагруженных силой тяжести буровых механизмов Pt 24 5 кН и направленной вверх технологической силой Р 60 кН. [7] |
Хорошо видно, что для исследованных условий при расчете моноопор из труб диаметром более 0 245 м необходимо учитывать динамический характер волнового давления. При волнении до 3 баллов для моноопор диаметром 0 299 м и более первая собственная частота колебаний при определенных высотах волн может совпасть с частотой волновой нагрузки. Для этих моноопор существуют резонансные режимы эксплуатации. [8]
Для получения результатов, наиболее точно отражающих влияние на напряженное состояние моноопоры технологической силы Р, эксцентриситета расположения механизмов е, установочного угла наклона ср моноопоры и смещения ai центра масс механизмов в процессе выполнения технологических операций, расчеты моноопор, эксплуатируемых по любым схемам, целесообразно выполнять численно. Численные методы универсальны и в отличие от приближенных не требуют предварительной аппроксимации формы изогнутой оси моноопоры функцией, которая хорошо описывает ее действительную форму, или использования каких либо других специальных приемов. Кроме того, они применимы к моноопорам с поперечным сечением, изменяющимся по ее высоте по любому закону. [9]
Поэтому при расчете моноопор следует применять стержневую модель. В механике стержней приняты в качестве аксиом следующие классические допущения. [10]
Для инженеров-практиков важно иметь в качестве итоговых расчетных формул простые математические выражения, позволяющие пусть и приближенно, но быстро и легко оценить напряженное состояние моноопоры. Применение теории бесселевых функций к расчету моноопор позволяет получить аналитическое решение уравнений типа (4.20) с необходимой точностью, но не в полной мере отвечает этим пожеланиям. [11]
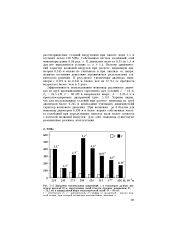 |
Диаграмма максимальных напряжений о в моноопорах разных диаметров высотой 18 м, нагруженных силой тяжести буровых механизмов Pt 24 5 кН и направленной вверх технологической силой Р 60 кН. [12] |
Собственная частота колебаний этой моноопоры равна 0 94 рад / с. Поэтому динамический характер волновой нагрузки при расчете моноопоры диаметром 0 245 м можно не учитывать и при анализе ее напряженного состояния допустимо ограничиться результатами статического решения. В результате увеличения диаметра моноопоры с 0 219 м до 0 245 м ( менее чем на 12 %) ее прочность возрастает более, чем в 3 раза. [13]
Для моноопоры переменного поперечного сечения из-за изменяющегося по высоте момента сопротивления наиболее опасным может стать сечение, в котором внутренний изгибающий момент может быть меньше максимального. Расчет моноопоры целесообразно начинать с определения ее напряженно-деформированного состояния в равновесном положении, т.е. со статического расчета, который выполняют, как правило, для всех проектируемых конструкций. Он позволяет получить первое общее представление об их работоспособности. В статическом расчете все действующие на моноопору нагрузки рассматриваются как квазистатические, т.е. постоянные во времени. Переменным во времени нагрузкам присваивается их максимальное значение. [14]
Бурение с моноопоры эффективно при угле поворота ее верхнего поперечного сечения не более, чем 10 ( 0 17 рад) от вертикали. В этой области расчет моноопоры допустимо выполнять по линейной теории изгиба, которая основана на предположении, что под действием нагрузок перемещения конструкции остаются малыми по сравнению с ее длиной, а квадраты углов ( в радианах) поворота оси моноопоры остаются малыми по сравнению с единицей. Использование линейной теории позволяет свести решение задачи к рассмотрению только линейных дифференциальных уравнений равновесия. [15]
Страницы: 1 2