Значение - коэффициент - подъемная сила
Cтраница 1
Значения коэффициентов подъемной силы носового и кормового крыльев на различных скоростях катера определяются исходя иэ принятых величин этих коэффициентов для его расчетной скорости. [1]
Значения коэффициентов подъемной силы, измеренные Олбумом [51], были поправлены с учетом влияния донного давления в предположении, что статическое давление на поверхности дна модели равно статическому давлению в набегающем потоке. [2]
Мы уже указывали, что для малых углов атаки формула Жуковского дает значение коэффициента подъемной силы, очень близкое к опытным данным; следовательно, формула ( 179), полученная математической обработкой физической гипотезы струйного обтекания ( гипотезы, впервые формулированной Гельмгольцем), дает при малых углах атаки ошибку в 4 раза ( преуменьшает подъемную силу пластины в 4 раза. [3]
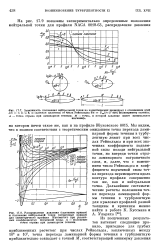
Мы видим, что в полном соответствии с теоретическим ожиданием точка перехода ламинарной формы течения в турбулентную лежит при всех числах Рейнольдса и при всех значениях коэффициента подъемной силы позади нейтральной точки, но впереди точки отрыва ламинарного пограничного слоя, и, далее, что с изменением числа Рейнольдса и коэффициента подъемной силы точка перехода перемещается вдоль контура профиля совершенно так же, как и нейтральная точка. [5]
Условие одинаковости отношения т / У 1 - М приводит к тому, что чем больше угол атаки, тем при меньших Мет можно ожидать совпадения расчетного и экспериментального значений коэффициента подъемной силы. [6]
Условие одинаковости отношения т / У 1 - MX приводит к тому, что чем больше угол атаки, тем при меньших Моо можно ожидать совпадения расчетного и экспериментального значений коэффициента подъемной силы. [7]
Условие одинаковости отношения т / У 1 - Мк приводит к тому, что чем больше угол атаки, тем при меньших Мао можно ожидать совпадения расчетного и экспериментального значений коэффициента подъемной силы. [8]
Значения коэффициента подъемной силы % оказались в широких пределах ( от 0 1 до 1 5), что объясняется разными условиями экспериментов или гипотезами в основе теоретических расчетов. [9]
Данная формула ( 22) получена из условия безотрывного обтекания потоком жидкости частицы. Для общего случая обтекания - с отрывом или без него - можно ввести коэффициент обтекания - , который при обтекании с отрывом пограничного слоя жидкости у поверхности частицы, очевидно, будет уменьшаться от 9 / 4 до нуля, аналогично тому, как снижается значение коэффициента подъемной силы у крыла самолета при достижении критического угла атаки. [10]
Данная формула ( 22) получена из условия безотрывного обтекания потоком жидкости частицы. Для общего случая обтекания - с отрывом или без него - можно ввести коэффициент обтекания - , который при обтекании с отрывом пограничного слоя жидкости у поверхности частицы, очевидно, будет уменьшаться от V - 9 / 4 до нуля, аналогично тому, как снижается значение коэффициента подъемной силы у крыла самолета при достижении критического угла атаки. [11]
Страницы: 1