Расчет - математическое ожидание
Cтраница 2
Количество шагов итерации определено требуемой точностью расчета математического ожидания числа пораженных воздушных целей. Как видно из табл. 10.3, при е 0 01 можно ограничиться четырьмя итерациями, при е 0 02 достаточно одной итерации. [16]
После накопления данных за время т производится расчет математических ожиданий и дисперсий накопленных случайных величин. Если же величина какой-либо дисперсии больше заданной, то продолжается накопление информации. Проверяется материальный и тепловой балансы. Он может не совпадать, если при математической обработке данных, накопленных за время т, машина допускает ошибку. В этом случае операции математической обработки повторяются. [17]
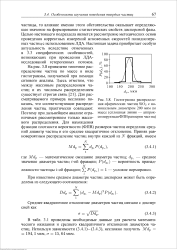 |
Гистограмма распределения сферических частиц SiC2 с номинальным диаметром 200 мкм по массе ( сплошная линия - аппроксимирующая ФПВ размеров частиц. [18] |
В табл. 3.1 приведены необходимые данные для расчета математического ожидания и среднего квадратичного отклонения диаметров частиц. Используя зависимости (3.4.1) - (3.4.3), несложно получить Mdp - 194 1 мкм, а 15 64 мкм. [19]
Полученные описанным способом значения вероятностей используют при расчете математического ожидания и дисперсии общего числа операций, необходимых для реализации отдельного законченного алгоритма. [20]
Денежные потоки проекта для каждого варианта и вероятность каждого варианта представлены в табл. 7.1. Результаты расчета математического ожидания денежных потоков приведены в последней строке. [21]
Если отдельные входы Xw и Zv не оказывают влияния на выход YJ, то они не будут учтены при расчете математических ожиданий и дисперсий, так как коэффициенты парной корреляции гх у. При практических расчетах, если коэффициент множественной корреляции порядка 0 85 - 0 9, то обычно определение характеристик может быть сделано с достаточной для практических целей точностью. [22]
Он отверг представление о рациональном экономическом субъ екте ( которые отстаивала школа Бентама и неоклассики) как о располагающем знанием всех возможных последствий своих действий определяющем стратегию сиоего поведения на основе некоторог расчета вероятного достижения конкретной заданной цели, анало гичного расчету математического ожидания. [23]
Движение отдельных частиц, в частности молекул, как правило, наиболее полно можно описать на языке квантовой механики - абстрактной математической теории, в которой все процессы, происходящие в природе, выражаются с помощью операторов физических величин. При этом сами операторы не дают наглядной физической картины, а конкретный физический смысл приобретают только средние значения или математические ожидания операторов, т.е. значения физических величин, получаемые в результате достаточно большого числа измерений. Расчет математических ожиданий, обычно обозначаемых парой угловых скобок, проводится согласно данной теории. Заметим, что во многих случаях имеет место формальное совпадение операторных уравнений с соответствующими уравнениями для математических ожиданий, хотя их смысл, вообще говоря, различный. Здесь, как правило, будем рассматривать математические ожидания физических величин ( операторов), поэтому там, где не возникает недоразумений, скобки, обозначающие математические ожидания, для краткости будем опускать. [24]
Суммирование их математических ожиданий дает математическое ожидание результирующей погрешности, а суммирование дисперсий частных погрешностей дает дисперсию результирующей погрешности. Если окажется, что суммарное математическое ожидание погрешности МВИ не равно нулю, то в МВИ целесообразно предусмотреть введение в результаты измерений поправки, равной с обратным знаком математическому ожиданию результирующей погрешности. Погрешность расчета математического ожидания результирующей погрешности полезно оценить. Если она окажется соизмеримой с остальными частными погрешностями, надо учесть ее как вырожденную случайную погрешность, равномерно распределенную з наибольшем интервале ее возможных значений. [25]
 |
Внутреннее кольцо - п к. [26] |
Изложенная в этой главе общая методика построения математических моделей технологических процессов дает возможность рассчитывать точность обработки для различных типов процессов, встречающихся на практике. Для наиболее характерных случаев, начиная с простейших операций, имеющих один вход и один выход, и кончая сложными процессами со многими входами и выходами, составлены расчетные таблицы. В этих таблицах для каждого варианта процесса приведены структурные схемы и соответствующие им уравнения связи и формулы для расчета математических ожиданий, дисперсий и практических полей рассеивания погрешностей обработки по заданным характеристикам исходных факторов заготовок и преобразующей системы. Каждой развернутой структурной схеме процесса соответствует эквивалентная матричная структурная схема. Формулы суммирования получены для общего случая, когда все анализируемые технологические факторы взаимно коррелированы между собой. [27]
Страницы: 1 2