Расчет - оптимум
Cтраница 1
Расчет оптимума заключается в следующем. [1]
Результаты расчета оптимума при 6 const и переменной F получаются примерно такими же, что и при q const я F const. [2]
Аналогичную схему расчета оптимума задачи (4.75) - (4.77) ввиду специальной формы целевой функции удается осуществить и в данном случае. Заметим, что, применительно к ЗОК, замыканием модели мы одновременно достигаем большего: осуществленное замыкание оказывается оптимальным в смысле принятого критерия оптимальности. [3]
Усиление практического значения расчета оптимума накопления и потребления с помощью аналитических формул требует постепенного усложнения моделей, приближения их к реальным условиям воспроизводственного процесса. [4]
 |
Пример крутого восхождения. [5] |
Отметим, что при расчете оптимума на электронно-вычислительных машинах ситуация часто по существу не отличается от ситуации в эксперименте. [6]
Так как на регулируемые параметры наложены ограничения типа неравенств, то расчет оптимума произведен методом прямого поиска с возвратом. [7]
Для того чтобы соответствующая, но не всегда сразу понятная интерпретация этих выражений была более ясной, мы выбираем здесь путь расчета оптимума для инвестора в модели двух ситуаций, который хочет разделить свое имущество на рисковое и безрисковое вложения. В заключение главы опять приводится задача, которая предназначена для применения приобретенных таким образом знаний. Необходимо будет определить критическую ставку процента применительно к рискованному проекту, хотя бы частично финансируемому заемным капиталом, а также квантифицировать влияние отношения к риску инвестора на эту ставку процента. [8]
Для того чтобы соответствующая, но не всегда сразу понятная интерпретация этих выражений была более ясной, мы выбираем здесь путь расчета оптимума для инвестора в модели двух, ситуаций, который хочет разделить свое имущество на рисковое и безрисковое вложения. В заключение главы опять приводится задача, которая предназначена для применения приобретенных таким образом знаний. Необходимо будет определить критическую ставку процента применительно к рискованному проекту, хотя бы частично финансируемому заемным капиталом, а также квантифицировать влияние отношения к риску инвестора на эту ставку процента. [9]
При оценке зависимости оптимального режима от малых параметров, не учтенных при поиске оптимума, также используется система уравнений типа ( 6) и ( 9), с той только разницей, что свободные члены в этих уравнениях находят дифференцированием по независимому параметру не тех уравнений, при помощи которых проводился расчет оптимума, а более общих уравнений, включающих в себя рассматриваемый малый параметр. Малый параметр может быть по своей природе как кинетическим, так и экономическим фактором; последний случай практически является наиболее важным, так как некоторые экономические характеристики, влияющие, хотя и не очень сильно, на положение оптимума, часто бывают неизвестны в начальной стадии проектирования. [10]
Показано, что преобразование координат позволяет устанавливать область оптимума при помощи простых графических методов. Приведен пример расчетов оптимума для следующих предельных значений параметров: содержание С02 85 %, избыток газа 600 % от стехиометрического количества, Ж: Т 7, температура 100 С. Проверены экспериментально два режима в оптимальной области и показано, что результаты эксперимента удовлетворительно совпадают с расчетными данными. [11]
При выборе любых из указанных выше варьируемых переменных в процессе оптимизации требуется рассчитать лишь реактор, котел № 2 и пароперегреватели. Однако после расчета окончательного оптимума следует убедиться, что создаваемого перегрева пара действительно достаточно для вращения воздуходувки. В примерах, рассматриваемых в этой главе, в качестве варьируемых переменных будут использованы значения температуры на входе в один или несколько слоев. [12]
На рис. ХП-2 не обозначены другие переменные, влияющие на работу установки, за которыми машина должна следить для соблюдения правил техники безопасности. Функции, показанные на рисунках, необходимы для расчета оптимума. [13]
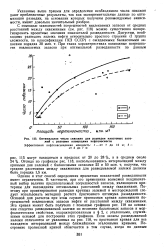 |
Оптимальное число скважин для разведки пластовых залежей с разными площадями нефтеносности. [14] |
Однако и этот способ определения проектных показателей разведанности имеет ограничения. В частности, при его применении возможен неоднозначный выбор величин предполагаемых погрешностей запасов, являющихся критерием для нахождения оптимальных расстояний между скважинами. По -, этому при проектировании разведки крупных залежей и месторождений следует использовать методику расчета прогнозного оптимума разведанности. Основой для расчетов при этом служит прогнозная кривая зависимости погрешностей извлекаемых запасов нефти от расстояний между скважинами. Эта кривая может быть получена с помощью графиков рис. 118 на основании сходства разведываемой залежи по величине балансовых запасов и морфологическим свойствам, охарактеризованным в § 2, с эталонными, служившими основой для построения этих графиков. Если запасы разведываемой залежи отличаются от указанных на рис. 118, то прогнозная кривая для нее находится интерполяцией между ближайшими эталонными кривыми. [15]
Страницы: 1