Расчет - плотность - жидкость
Cтраница 1
Расчет плотности жидкости в атмосферных условиях, состав которой приведен в табл. IV. С дается в примере IV. Плотность подсчитывается двумя способами: методом аддитивных объемов и методом Стендинга и Каца. Такое совпадение результатов объясняется небольшим процентным содержанием метана и этана в смеси. [1]
Расчеты плотностей жидкостей основаны обычно на вычислении значений плотности, усредненных по составу. Такой подход требует только внимательного отношения к единицам физических величин, используемых в расчете. [2]
Для расчета плотности жидкости при пластовых условиях по составу смеси необходимо знать ее сжимаемость и тепловое расширение. Методика такого расчета приведена в примере IV. [3]
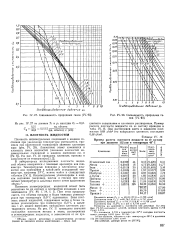 |
Сжимаемость природных газов [ IV. 93 ]. [4] |
Пример расчета плотности жидкости по ее составу приведен в табл. IV. При растворении азота в жидкости плотностью 0 68 г / см3 его кажущаяся плотность составляет 0 48 е / сжз. [5]
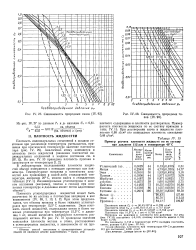 |
Сжимаемость природных газоъ [ IV. 93 ].| Сжимаемость природных газов [ IV. 93 ]. [6] |
Пример расчета плотности жидкости по ее составу приведен в та бл. При растворении азота в жидкости плотностью 0 68 г / см3 его кажущаяся плотность составляет 0 48 г / смз. [7]
Для расчета плотностей промоочной жидкости из условия УСТОЙЧИВОСТИ стенок скаажены, гидроразрыва и создания нэрмаяьног. [8]
Величины, необходимые для расчета плотности жидкости при температуре кипения, обычно неизвестны. [9]
Перед ОПЗ необходимо контролировать качество жидкости в интервале перфорации поинтервальным замером давления и расчетом плотности жидкости или отбором проб желонкой. [10]
Прогнозы сжимаемости жидкостей достаточно точны для расчетов фугитивно-стей, чего нельзя сказать о расчетах плотностей жидкостей; так, уравнение Соава может дать результат на 10 - 20 % ниже действительного, уравнение Пенга - Робинсона является чуть более точным. Эти методы эффективны при проведении расчетов режимов охлаждения, очистных смесей и фазовых равновесий при давлениях вплоть до 350 атм. [11]
Прогнозы сжимаемости жидкостей достаточно точны для расчетов фугитивно-стей, чего нельзя сказать о расчетах плотностей жидкостей; так, уравнение Соава может дать результат на 10 - 20 % ниже действительного, уравнение Пенга - Робинсона является чуть более точным. Эти методы эффективны при проведении расчетов режимов охлаждения, очистных смесей и фазовых равновесий при давлениях вплоть до 350 атм. [12]
В статье дан анализ, основанный на 2500 экспериментально найденных значениях констант равновесия уравнений Соава, Пенга - Робинсона, Бенедикта - Уэбба - Рубина - Старлинга, а также разработанного Маккарти уравнения, основанного на принципе соответственных состояний ( МПСС), включающего 33 константы. Проведен сравнительный анализ значений плотности пара и жидкости, констант равновесия и точек росы. Как установлено, для расчета плотности жидкостей уравнение соответственных состояний Маккарти и уравнение Бенедикта - Уэбба - Рубина - Старлинга несомненно более приемлемы, чем другие более простые уравнения, однако при прогнозировании прочих перечисленных свойств преимущество этих уравнений не так явно выражено. [13]
В статье дан анализ, основанный на 2500 экспериментально найденных значениях констант равновесия уравнений Соава, Пенга - Робинсона, Бенедикта - Уэбба - Рубина - Старлинга, а также разработанного Маккарти уравнения, основанного на принципе соответственных состояний ( МПСС), включающего 33 константы. Проведен сравнительный анализ значений плотности пара и жидкости, констант равновесия и точек росы. Как установлено, для расчета плотности жидкостей уравнение соответственных состояний Маккарти и уравнение Бенедикта - Уэбба - Рубина - Старлинга несомненно более приемлемы, чем другие более простые уравнения, однако при прогнозировании прочих перечисленных свойств преимущество этих уравнений не так явно выражено. [14]
Данная работа посвящена главным образом тем уравнениям, которые применимы при криогенных температурах. В общем, случае для описания систем, плотность которых в 0 75 раз превышает критическую, можно применять вириальное уравнение, усеченное по члену С. Цонопулос и Праузниц рассматривают несколько уравнений, пригодных для расчета плотности жидкостей. Уравнение Битти - Бриджмена пригодно для описания систем, плотность которых приблизительно равна критической, а уравнение Бенедикта - Уэбба - Рубина - для представления систем при плотностях, превышающих критическое значение не более чем в 1 8 раз. Вариант уравнения Бенедикта - Уэбба - Рубина, разработанный Стропбриджем, был применен для описания жидкости, плотность которой втрое больше критической. Вариант уравнения Ван-дер - Ваальса, в состав которого включена двадцать одна константа, можно использовать для расчета свойств жидкостей, плотность которых вдвое превышает критическую. Для расчетов величин энтальпии и коэффициентов равновесия испарения в интервале криогенных температур пригодны, как установлено, несколько вариантов уравнения Редлиха - Квонга, включающих параметры бинарного взаимодействия. После опубликования этой статьи для описания криогенных жидкостей были применены уравнения типа Бенедикта - Уэбба - Рубина, в которые входят тридцать - сорок констант, разработанных Вендором и Гудвином, а также предложенное Маккарти уравнение соответственных состояний, в состав которого входит множество констант. [15]
Страницы: 1 2