Расчет - электромагнитные поля
Cтраница 1
Расчет электромагнитных полей в равномерно-изогнутых волноводах сложной формы поперечного сечения рассматривался в [5], в которой решение получено с помощью метода частичных областей. Расчет проводился в предположении о возможности независимого распространения в волноводе сложной формы волн Е - и Н - типов ( относительно оси z в цилиндрической системе координат), которое справедливо только при расчете критических частот и не выполняется при определении постоянной распространения в равномерно-изогнутом волноводе сложной формы поперечного сечения. Вопросы учета связи Е - и Я-решений обсуждались в [5], В [89] решение этой задачи проводится с использованием вариационного метода. [1]
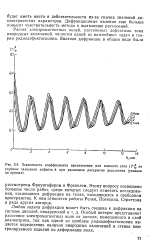 |
Зависимость коэффициента прохождения для плоского слоя Т от глубины залегания дефекта Л при различном раскрытии расслоения ( указано на кривых. [2] |
Расчет электромагнитных полей, рассеянных дефектами типа инородных включений, является одной из важнейших задач в теории радиодефектоскопии. [3]
Расчет электромагнитных полей производится при помощи уравнений, выведенных Максвеллом. [4]
Расчет двумерных электромагнитных полей легко обобщается на расчет полей в соответствии с формулами (14.56) в трехмерных областях. На рис. 14.65 изображены ячейка трехмерной пространственной сетки и точки определения узловых значений, составляющих напряженности электрических и магнитных полей. Узлы электрического поля расположены в середине ребер ячейки, а магнитного поля - в центре ее граней. [5]
При расчете электромагнитных полей в электрических машинах пользуются уравнениями Максвелла, которые устанавливают связь между электрическими и магнитными величинами. Кроме этих четырех векторов, материальная среда характеризуется источниками электромагнитного поля. Такими источниками являются электрические заряды и токи. [6]
При расчете электромагнитных полей иногда удобно заменить их истинные источники ( электрические токи) на эквивалентные магнитные. Со времен Ампера известна возможность замены замкнутого контура с током магнитным дипольным моментом. Однако традиционное изложение этого вопроса в курсах классической электродинамики ( см., например, [11]) представляется нам несколько искусственным. Более логичным выглядит подход, базирующийся на систематическом введении магнитных токов j 77) в уравнения Максвелла. [7]
При расчете электромагнитных полей конкретных источников, находящих практическое использование, обычно необходимо получить ответ на следующие вопросы. [8]
Излагаются методы расчета электромагнитных полей и теория регулярных полосковых волноводов. Эти результаты положены в основу проектирования и расчета элементов, узлов н малогабаритных устройств полосковой аппаратуры СВЧ, изложенных ее второй части пособия. Приведенные расчетные соотношения хорошо согласуются с опытными данными и удобны для практического применения. [9]
Излагаются методы расчета электромагнитных полей и теория регулярных полосковых волноводов. Теоретические и экспериментальные данные, приведенные в первой части пособия, позволяют рассчитать основные рабочие параметры полосковых волноводов. Эти результаты положены в основу проектирования и расчета элементов, узлов и малогабаритных устройств полосковой аппаратуры СВЧ, изложенных во второй части пособия. Приведенные расчетные соотношения хорошо согласуются с опытными данными и удобны для практического применения. [10]
Излагаются методы расчета электромагнитных полей и теория регулярных полосковых волноводов. [11]
Приведены методы расчета электромагнитных полей в основных элементах магнитной цепи машины и в наиболее нагруженных конструктивных элементах. Рассмотренные решения ряда практических задач, возникающих при проектировании новых типов машин, могут служить справочным материалом. Книга весьма актуальна и имеет большое прикладное значение в условиях возрастающих требований к точности расчета электромагнитных полей в крупных машинах. [12]
Наряду с расчетом электрических, магнитных и электромагнитных полей имеет большое практическое значение их непосредственное экспериментальное исследование в реальных устройствах, а также их экспериментальное исследование методом моделирования. [13]
Кратко рассмотрим схему расчета электромагнитных полей в нелинейной среде, когда в рамках определенных предположений удается ввести линеаризованную, но нестационарную модель электродинамических свойств вещества. Излагаемый далее подход хорошо известен в нелинейной оптике. [14]
Метод используется для расчета электромагнитных полей внутри проводящих тел и является полуаналитическим, так как представляет собой аппроксимацию непрерывных распределений параметров многозвенной цепью определенной структуры. Рассмотрим сначала случай цилиндрической круговой или овальной оболочки, толщина которой по всему периметру значительно меньше глубины проникновения. [15]
Страницы: 1 2 3 4