Расчет - адсорбционный процесс
Cтраница 1
Расчет адсорбционных процессов предполагает наличие кинетических уравнений, выражающих величину адсорбции как функцию времени осуществления реального процесса. [1]
Расчет адсорбционных процессов в неподвижном слое адсорбентов предлагается осуществлять с учетом двух основных факторов, влияющих на характер развития процесса: нелинейности изотермы адсорбции и кинетики, определяемой внутренней и продольной диффузией. Представлены аналитические решения вну-тридиффузионных процессов адсорбции на зернах различной геометрии для произвольной нелинейной изотермы с постоянным и переменным эффективными коэффициентами диффузии, функционально зависимыми от степени заполнения адсорбционного пространства адсорбатом. Установлена связь между кинетическими и равновесными характеристиками процесса. [2]
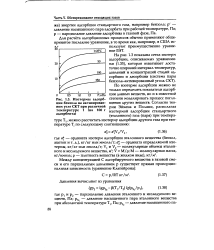 |
Изотермы адсорбции бензола на активированном угле СКТ при различной температуре t ( на 100 г адсорбента. [3] |
Для расчета адсорбционных процессов обычно применяют общепринятое последнее уравнение, в то время как, например, в США используют преимущественно уравнение БЭТ. [4]
Основные принципы расчета адсорбционных процессов и выбора рационального режима ведения таких процессов освещены также в статье Н. А. Измайлова, Ю. В. Шостенко и С. К сожалению, в этой статье опыт йодной промышленности не использован. [5]
 |
Зависимость массы в тад адсорбиро - тпаа, кг / кг ванного на древесном угле этчлхлорида от дав - О В ления Р при различной температуре t. [6] |
В СССР для расчета адсорбционных процессов применяют последнее уравнение, в то время как, например, в США используют преимущественно уравнение БЭТ. [7]
Основная задача описания и расчета адсорбционного процесса, с точки зрения практики, состоит в определении концентрации целевого компонента в газе-носителе на выходе из слоя адсорбента. В научном плане физико-математический анализ процесса периодической адсорбции в условиях неподвижного слоя имеет своей целью получение нестационарных распределений концентрации целевого компонента в газовой фазе и в дисперсном адсорбенте по высоте слоя, а для непрерывных процессов в движущихся и псевдоожиженных слоях - получение стационарных распределений концентрации. [8]
Закон Генри находит применение в расчетах адсорбционных процессов. [9]
Следует отметить, что до сих пор расчет адсорбционных процессов базировался на линейных формах изотермы. Так как в реальных процессах адсорбции изотермы нелинейны, рядом исследователей были предприняты попытки использовать нелинейные модели изотерм. [10]
Одним из наиболее информационно насыщенных прикладных методов расчета адсорбционных процессов является расчет динамики адсорбции, позволяющий рассчитать выходную кривую процесса, то есть изменение концентрации адсорбтква С на выходе из слоя адсорбента во времени С, определить время условного проскока адсорбтива в рафинат, время полной отра - ботки слоя адсорбента te и другие технологические параметры. Основой расчета динамики сорбции является уравнение изотермы адсорбции и уравнения, описывающие массообмен в условиях лимитирующего диффузионного сопротивления. Многообразие исходных уравнений затрудняет их отбор для выполнения конкретных расчетов; ошибочный выбор уравнения, учитывающего специфический вид диффузионного сопротивления, приводит к существенным погрешностям расчета выходных параметров. [11]
Изученные явления требуют учета эффективного размера молекул при выборе рациональных адсорбентов, причем в ряде случаев невозможно проводить расчеты адсорбционных процессов с использованием констант, определенных по бензолу. [12]
Для расчета адсорбционных процессов используются приближенные методики. [13]
В настоящее время не получены надежные критериальные уравнения для определения коэффициентов массопередачи при адсорбции многокомпонентных смесей. Поэтому для расчета адсорбционных процессов в настоящее время используются приближенные методики. [14]
Оба выражения - ( 162) и ( 163) - - в ректификации представляют собой одну и ту же величину относительной летучести. В адсорбции из отношения ( 161) выражение ( 163) получено быть не может. Однако в расчетах адсорбционных процессов отношение, аналогичное уравнению ( 163), фигурирует; оно называется коэффициентом распределения, или разделения. Этот коэффициент следует обозначать отлично от адсорбционного коэффициента относительной летучести, например ар. [15]
Страницы: 1 2