Расчет - сетка
Cтраница 2
Лишь формальные соображения ( задано 8 функций ( р) - имеется произвол в 8 функций) и большой опыт расчетов сеток подтверждает гипотезу о существовании таких теорем. [16]
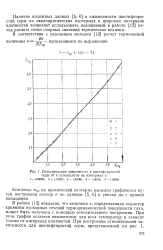 |
Относительная зависимость е шестифтор истой серы от е углекислоты на изотермах т. [17] |
Наличие надежных данных [5, 6] о сжимаемости шестифтори-стой серы на околокритических изотермах в широком интервале плотностей позволяет использовать изложенный в работе [12] метод расчета сетки опорных значений термических величин. [18]
J указывает, что в практике электромоделирования вполне удовлетворительные результаты получают при использовании более удобной для расчетов методики определения параметров переходных зон, базирующейся на методе расчета асимметричных сеток, изложенном в § 3 данной главы. На рис. 20, б показаны прямоугольная сетка с ячейками разной величины и переходная зона. [19]
В [27] тот же метод разбиения проводников заземлителя на небольшие участки с последующим расчетом на ЦВМ распределения заряда ( тока) между ними был применен к расчету прямоугольных заземляющих сеток. [20]
Остановимся кратко на прямых конформных и равнопромежуточных конических проекциях. При расчете сеток прямых конич. Кроме того применяются плоские прямоугольные координаты - абсцисс х и ординат у с осью х, совпадающей с полярной осью первой системы, и началом координат в точке пересечения этой оси с одной из параллелей. [21]
Поправка Флори учитывает длинные свободные концы макромолекул, поэтому в сетках с высокой плотностью без большой погрешности ими можно пренебречь. Таким образом, для расчета сетки по вышеприведенным формулам необходимо найти значение параметров / и q2m; при отсутствии литературных данных величины у и 4im требуют экспериментального определения. [22]
Главный недостаток этих численных методов моделирования обмена массами в тесных двойных состоит в том, что они требуют огромного времени счета на больших машинах. Кроме того, как указали Любов и Шу, возможно, что используемые в таких расчетах сетки все еще слишком грубы и не дают надежных результатов, поскольку эффекты давления могут играть важную роль на расстояниях, сравнимых с шагом сетки. [23]
 |
Схема идеальной тетрафункциональной.| Схема узла тетра ( 1 и трифункциональной ( II сетки. [24] |
Изучение некоторых свойств сшитых полимеров ( например, набухания, растворимости, растяжения ли сжатия) позволяет находить структурные параметры сетки, знание которых дает возможность грамотного подбора мономеров и олигомеров для создания полимеров с регулярной структурой и заданными свойствами [1], качественно прогнозировать физико-химические и ( Механические свойства материалов [2-12], определять термодинамический параметр взаимодействия полимер - растворитель и вычислять второй вириальный коэффициент А2 [13, 14], необходимые для расчетов в теории растворов полимеров. В недавно вышедшем обзоре [1] подробно рассматриваются вопросы формирования сетчатых структур в процессах синтеза, разбирается связь гелеобразо-вания со степенью конверсии функциональных групп мономеров, особенности формирования сеток на различных стадиях реакции, регулируемый синтез сетчатых полимеров и др. Поэтому в настоящем обзоре эти вопросы не затрагивались, а поставленная задача ограничивалась рассмотрением методов расчета сеток, образованных как в процессах синтеза, так и старения под действием различных агентов. [25]
Размеры таких зон могут быть существенно меньше характерного линейного размера задачи, а их местонахождение заранее неизвестно и, кроме того, может меняться в процессе расчета. В связи с этим разрабатываются алгоритмы, к-рые позволяли бы использовать в расчетах сетки, сгущающиеся в таких зонах. [26]
Суть изменений сводится к тому, что расчет параметров течения на следующем временном слое проводится в узлах неподвижной эйлеровой сетки. После этого сетка перестраивается таким образом, что внутренние лучи буферной зоны ( Fp и Fv на рис. 12.52) совмещаются с лидирующими точками детонационной или ударной волн, перемещающимися в соответствующих направлениях. Параметры в узлах новой сетки определяются путем интерполяции. Использование в расчетах дискретно-подвижной сетки позволяет получать устойчивые решения задач детонации кумулятивных зарядов при использовании полупроцентного сглаживания. [27]
Весовую долю золь-фракции сшитого полимера находят по уравнению ( 1), измеряя содержание геля. Действительно, на практике для значительных доз облучения получают прямую или асимптотически приближающуюся к ней кривую - Уравнение ( 22) было предложено впервые для полиэтилена с исходным наиболее вероятным МБР. Поэтому при малых дозах облучения возможно отклонение от линейной зависимости, вследствие отличия распределения в образце от наиболее вероятного. Таким образом, для расчета сетки в этом случае необходимо измерение s в широком диапазоне доз облучения. В отличие от прочных, необратимых при разрушении кова-лентных связей, образующих трехмерные структуры, физические узлы являются неустойчивыми ( лабильными), способными восстанавливаться после разрушения. Полимеры с большим количеством физических узлов, проявляющие при определенных условиях свойства сетки, считают квазисетчатыми. [28]
При решении задач первой группы в полной мере проявляются достоинства ПЛЭ метода. Дополнительно возникает лишь вопрос построения сеток. Ко второй группе относятся задачи с большими формоизменениями оболочки. Поэтому при их решении не удается избежать трудностей, которые связаны с использованием в расчете сеток различной структуры. [29]
Страницы: 1 2