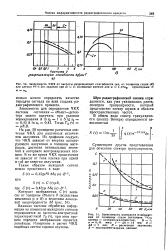
Расчет - подобная система
Cтраница 2
Если принять спицы нерастяжимыми, что часто допускается в расчетах подобных систем, то решение уравнений ( 53) резко упрощается. [16]
Хотя с практической точки зрения весьма существенное значение имеет стабилизация пламени струями, как это видно из обзорной статьи Кембела, помещенной в третьем разделе сборника, в настоящее время общие методы расчета подобных систем отсутствуют. [17]
 |
Энергетическая диаграмма, образования молекулы водорода. [18] |
Метод молекулярных орбиталей ( МО) сводится к рассмотрению состояния двух или нескольких электронов относительно двух или более ядер, так как он предполагает, что молекула есть система с обобщенными электронами и ядрами. Расчет подобных систем ведется по уравнению Шредингера с соответствующими допущениями, так как точное решение, как известно ( с. [19]
В данной книге нашли отражение вопросы теории и практического применения аналитического варианта МГЭ применительно к одномерным плоским и пространственным расчетным схемам линейных систем стержней и пластин. Для расчета подобных систем предложен вариант МГЭ, основанный на новой схеме преобразования интегральных соотношений метода начальных параметров в систему линейных алгебраических уравнений. Отличительной особенностью метода является единообразный подход к алгоритму задач статики, динамики и устойчивости, что создает широкие возможности для машинной реализации алгоритма. Показано, что решения этих трех типов задач отличаются только лишь фундаментальными функциями, а матричная форма разрешающих уравнений позволяет совместить разные задачи. Несмотря на уклон в задачи строительной механики и теории тонких пластин, разработанный аналитический вариант МГЭ с небольшими изменениями может быть приспособлен для решения задач электротехники, теплотехники, физики, гидрогазодинамики, аэроупругости и других наук, где соответствующие процессы можно описать дифференциальными уравнениями. [20]
Для расчета подобных систем часто используется подход, который был разработан существенно раньше для приборов с дискретным взаимодействием. [21]
В данной книге нашли отражение вопросы теории и практического применения аналитического варианта МГЭ применительно к одномерным плоским и пространственным расчетным схемам линейных систем стержней и пластин. Для расчета подобных систем предложен вариант МГЭ, основанный на новой схеме преобразования интегральных соотношений метода начальных параметров в систему линейных алгебраических уравнений. Отличительной особенностью метода является единообразный подход к алгоритму задач статики, динамики и устойчивости, что создает широкие возможности для машинной реализации алгоритма. Показано, что решения этих трех типов задач отличаются только лишь фундаментальными функциями, а матричная форма разрешающих уравнений позволяет совместить разные задачи. Несмотря на уклон в задачи строительной механики и теории тонких пластин, разработанный аналитический вариант МГЭ с небольшими изменениями может быть приспособлен для решения задач электротехники, теплотехники, физики, гидрогазодинамики, аэроупругости и других наук, где соответствующие процессы можно описать дифференциальными уравнениями. [22]
Влияние системы обработки информации на изменение выходного сигнала определяется ее частотно-контрастной характеристикой Те ( v), при этом процесс передачи изображения является линейным. Измерение и расчет ЧКХ подобных систем хорошо изучены. [24]
Статические расчеты существенно нелинейных систем - обла-дают рядом отличительных особенностей. В настоящей главе расчеты подобных систем выполнены графическим методом. [25]
Имеются сообщения [84, 74] о расчетах методом Монте-Карло бинарных смесей твердых сфер различных диаметров. Кроме того, существуют расчеты подобных систем методом молекулярной динамики [3], которые можно использовать для сравнения. Обозначим через ai и а2 ( at а2) диаметры молекул, через NI, Nz и V - число молекул и полный объем. [26]
 |
Общая схема замкнутой системы автоматического управления. [27] |
Если звено с насыщением или ограничением находится перед звеном с большой инерцией, то существенного увеличения быстродействия можно достигнуть работой почти полностью на нелинейных участках. Существует два подхода к расчету подобных систем. В первом случае на L-плоскости изображается изменение усиления разомкнутой системы в функции амплитуды колебаний, и выбирается такая нелинейная обратная связь, чтобы система всегда оставалась устойчивой и имела максимально возможную резонансную частоту. Во втором случае по уравнению переходного процесса торможения, который заканчивается при ошибке и всех ее производных, равных нулю, строится предсказатель. Этот предсказатель наивыгоднейшего момента переключения с максимальной мощности на максимальное торможение содержит нелинейные вычислительные устройства для расчета динамики выходного инерционного звена. На предсказатель подаются производные входного сигнала и сигнала обратной связи. Дифференцирующие цепи можно рассчитывать по соображениям полосы пропускания или статистически. [28]
Выражения (6.27) и (6.28) характеризуют динамическую нагрузку в соединительных канатах и поднимаемой высотной металлоконструкции при изменении возмущающих сил по синусоидальному закону. Эти зависимости могут быть использованы для расчетов подобных систем. [29]
Структурная схема системы в практическом выполнении оказывается, как правило, сложной, что обусловлено часто наличием нескольких цепей обратной связи и нескольких входных звеньев. Несколько цепей применяется из-за самого характера проблемы управления, и инженер должен быть подготовлен для анализа и расчета подобных систем. [30]
Страницы: 1 2 3