Расчет - упругая система
Cтраница 1
Расчет упругих систем на устойчивость при повышенных температурах важен прежде всего для авиационных конструкций. Аэродинамический нагрев обшивки летательных аппаратов, имеющих сверхзвуковую скорость полета, приводит к неравномерному распределению температур в конструкции; появляющиеся при этом термические сжимающие напряжения могут вызвать потерю устойчивости элементов обшивки. [1]
Расчет упругих систем с учетом паразитных колебаний заключается прежде всего в определении всех частот свободных колебаний ( практически можно определить парциальные частоты), с целью сохранения определенной дистанции между рабочими и паразитными частотами. Частоты определяются согласно табл. 5 и ( 9) - ( 11) для цилиндрических пружин и по ( 29) для рессор. [2]
Практика расчетов упругих систем показывает, что в подавляющем большинстве случаев те упрощения, которые делались в рассмотренных выше задачах, являются неприемлемыми. Так, большей частью собственная масса упругих связей ( балок, валов) оказывается соизмеримой с присоединенными массами. Последние же в свою очередь редко удается рассматривать как сосредоточенные. [3]
Современная теория расчета упругих систем пока еще не учитывает ряд факторов, влияющих на усилия, возникающие в реальных трубопроводах. [4]
Одним из эффективных методов расчета нелинейно упругих систем является шаговый метод, который заключается в следующем. [5]
Выбор того или иного метода приближенного расчета зависит как от вида подлежащей расчету упругой системы, так и от тех требований, которые предъявляются к точности расчета. [6]
Основной метод приближенного расчета удара - метод приведения массы - - позволяет свести расчет сложной упругой системы к расчету системы с одной степенью свободы. [7]
Основным методом приближенного расчета удара является так называемый метод приведения массы, который дает возможность расчет сложной упругой системы свести к расчету системы с одной степенью свободы. [8]
 |
Расчетная схема. [9] |
Каждый ригель рамы разбивался на несколько равных участков. Согласно полученному из расчета упругой системы ( на осадку 1см) распределению усилий, на каждом участке определялась средняя величина действующего момента. [10]
К сожалению, нет еще достаточно строгой и сколь-либо удовлетворительной теории разрушения материалов. Многочисленные теории прочности, применяемые в расчетах упругих систем, теряют силу при приложении их к расчету не вполне упругих систем, где существенное значение имеют и время действия сил на тело, и скорость, с которой эти тела подвергаются деформированию. [11]
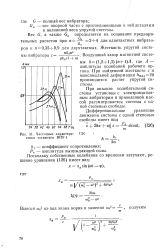 |
Частотные характеристики установки ВПУ-1. [12] |
Воздушный зазор магнитной системы 6 ( 1 2 - М 3) ( п 1) Л, где Л - амплитуда колебаний рабочего органа. При найденной жесткости с и максимальной деформации / гтах26 производится расчет упругой системы. [13]
Точность динамического расчета зубчатых передач определяется принятой моделью динамической системы и ее параметрами. Сама процедура динамического расчета зубчатых передач после получения системы дифференциальных уравнений, описывающих их динамическое состояние, не отличается от разработанных в теории колебаний аналитических и численных методов расчета упругих систем. [14]
Для определения напряжения о необходимо проинтегрировать это уравнение при соответствующих начальных условиях. По предположению, мгновенные деформации упруги, поэтому начальные напряжения [ ах ( t 0) aj, ет2 ( f - 0) а § находятся из расчета идеально упругой системы. Этот расчет очень прост. [15]
Страницы: 1 2