Расчет - спектр
Cтраница 3
Были проведены расчеты спектров временных рядов, представляющих собой ежемесячные замеры дебита конденсата на отдельных скважинах месторождения Южный Мубарек. Форма спектра выявляет особенности временного ряда, которые должны быть учтены в любой модели, предложенной для этого ряда. Наличие пиков в спектре и их величины могут выявить основные периодичности, имеющие физическое объяснение. [31]
Данный метод расчета спектра основан на анализе корреляционной матрицы сигнала, поэтому прежде всего необходимо определить эту матрицу. Если х - вектор отсчетов сигнала, формированием корреляционной матрицы управляют параметры Nwin и Noverlap. Параметр Nwin может быть числом, обозначающим размер прямоугольного окна, или вектором, содержащим коэффициенты окна. Сигнал делится на фрагменты в соответствии с длиной окна ( равной Nwin или length ( Nwin)), при этом перекрытие соседних фрагментов составляет Noverlap отсчетов. [32]
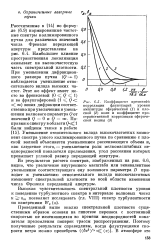 |
Коэффициент временной корреляции флуктуации уровня амплитуды сферической ( 7 и плоской ( 2 волн и коэффициент пространственной корреляции сферической волны ( 3. [33] |
Из результатов расчета спектров, изображенных на рис. 6.6, видно, что увеличение внутреннего масштаба или эквивалентное уменьшение соответствующего ему волнового параметра D приводит к уменьшению относительного вклада высокочастотных компонент спектральной плотности во всей области изменения числа Френеля передающей апертуры. [34]
Известны попытки расчета спектров ионных серий с периодами, отличными от 14 ( 12, 13, 15, 16, 29 и другие) [31], однако аналитические возможности такого подхода пока еще не ясны и применение таких спектров затруднительно без дальнейших исследований в этой области. [35]
Если при расчете спектра используется весовая функция ( окно) с коэффициентами w ( k), формула (5.21) слегка модифицируется - вместо числа отсчетов NE знаменателе должна стоять сумма квадратов модулей коэффициентов окна. [36]
Кроме того, расчет спектра ЭПР из три-диагональной матрицы Фи необходимо делать несколько раз. Мы предлагаем другой способ выбора размерности базиса Лан-цоша, причем этот способ не требует дополнительных затрат времени и оперативной памяти. На каждом шаге алгоритма Ланцоша строится базисный вектор т), ортогональный к двум предыдущим. В связи с этим в работе [6] рассмотрены возможности реортогонализации базиса с целью получения большего числа собственных значений и собственных векторов с нужной точностью. Отметим, что 1 1) 1; Ч 2) 0; ( 11 3 ci 10 - le, что соответствует точности машинного представления действительных чисел в арифметике 8-байтных чисел. Более того, нет необходимости проверять ортогональность нового базисного вектора ко всем остальным, поскольку такой способ требовал бы хранения всего базисного набора и заведомо нерационален. Мы проверяем ортогональность каждого нового базисного вектора лишь по отношению к стартовому вектору. [37]
Таким образом, расчет спектров ЭПР на электронной вычислительной машине после соответствующей обработки позволяет сделать полезные качественные рекомендации относительно приближенного анализа неразрешенных и асимметричных спектров ЭПР; кроме того, открываются возможности для более строгого анализа спектров ЭПР. Можно надеяться, что сочетание различных методов анализа при наличии набора ( рафиков теоретических спектров и номограмм позволит производить падежную расшифровку и обработку самых различных спектров ЭПР, а это значительно расширит возможности применения метода ЭПР для решения различных научных вопросов. [39]
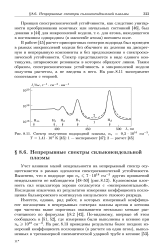 |
Спектр излучения водородной плазмы, пе 9 3 101 Т 1 41 104 К. 1 - эксперимент. 2 - расчет. [40] |
В работе [45] расчет припороговых спектров водорода был проведен в рамках микрополевой модели без обычного их деления на дискретную и непрерывную компоненты и без предположения о спектроскопической устойчивости. Спектр представляется в виде единого континуума, штарковские резонансы в котором образуют линии. Таким образом, спектроскопическая устойчивость в микрополевой модели получена расчетом, а не введена в него. На рис. 8.11 эксперимент сопоставлен с теорией. [41]
Далее обсуждаются методы расчета спектра. Если спектр квантовой системы уже известен, то сравнительно несложно установить, какой вклад в него вносит та или иная периодическая орбита. Для этого была развита мощная техника ресуммирования, позволяющая избежать расходимостей, связанных с экспоненциальным увеличением числа периодических орбит с ростом их длины. [42]
Предпринятые недавно попытки расчета спектров слюд с учетом всех колебаний кристалла [1] не привели к однозначной интерпретации. Представлялось необходимым: а) обращение к спектрам простых слоистых силикатов M2Si205 и MSi205 с небольшим числом атомов в ячейке ( их полуэмпирическая интерпретация рассмотрена ранее [2-4]) и б) исследование спектров монокристаллов для получения сведений об ориентации моментов переходов. [43]
В первоначальном [3] расчете спектра этого полимера ( на основе экспериментального спектра, снятого на частоте 60 МГц) использовались параметры, несколько отличные от указанных, и звенья с / - конфигурацией не были обнаружены. Соответствие между экспериментальным и рассчитанным спектрами было менее удовлетворительным, главным образом, потому, что для спектров, снимаемых на более низкой частоте, шестиспиновая модель является менее удовлетворительным приближением. [44]
 |
Решетка Бете, или дерево Каули, ( а и кактусовая модель Фуши-Ми с координационным числом 4 ( б. [45] |
Страницы: 1 2 3 4
