Расчет - эффективная теплопроводность
Cтраница 1
Расчет эффективной теплопроводности по эмпирическим формулам ( 5 - 15), ( 5 - 16) обычно требует постановки экспериментов для определения эмпирических коэффициентов для каждого конкретного материала. [1]
Расчет эффективной теплопроводности увлажненных или воздушно-сухих материалов проводится в несколько этапов, последовательность которых определяется характером структуры волокнистого материала и местами сосредоточения влаги. [2]
Результаты расчета эффективной теплопроводности по формулам ( 3 - 9), ( 3 - 41) сопоставлены на рис. 3 - 13 - 3 - 20 и в табл. 3 - 2 с экспериментальными данными для различных природных и искусственных зернистых материалов в широком диапазоне изменения параметров. [3]
Помимо расчетов эффективной теплопроводности, проведенных с помощью ЭЦВМ, в 1965 г. нами были выполнены исследования на электрической аналоговой машине. [4]
Итак, расчет эффективной теплопроводности объемных волокнистых материалов с хаотической структурой проводится по следующей схеме: по формулам ( 5 - 8), ( 5 - 12), ( 5 - 5) определяется теплопроводность газовой компоненты между волокнами Я2м; затем по формуле ( 1 - 32) вычисляется эффективная теплопроводность. [5]
Поэтому при расчете эффективной теплопроводности зернистых систем в состоянии свободной засыпки, на наш взгляд, следует говорить о зоне предсказываемых расчетом значений, ширина которой обусловлена степенью достоверности сведений об определяющих параметрах. [6]
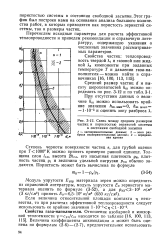 |
Связь между средним размером. [7] |
Перечислим исходные параметры для расчета эффективной теплопроводности и приведем рекомендации и справочную литературу, содержащую указания о численных значениях рассматриваемых параметров. [8]
В табл. 6 приведены результаты расчета эффективной теплопроводности полукокса в интервале температур 450 - 650 С при фильтрации через него летучих продуктов полукоксования. Полученные величины имеют один порядок, и разбег их от 0 327 до 0 713 ккал / м-ч - град обусловлен качеством полукокса и интенсивностью выделения летучих продуктов. Так же как и при сушке сланца видна тенденция к повышению Я. [9]
В табл. 5 помещены результаты расчета эффективной теплопроводности сухого сланца в период сушки. Полученные величины имеют один порядок, а некоторый разбег их обусловлен неоднородностью состава образцов. [10]
Необходимо остановиться подробнее на методике расчета эффективной теплопроводности твердых капиллярнопористых тел. Для двухфазной системы, твердая фаза которой состоит из двух или более компонентов, может быть рекомендована следующая методика расчета. [11]
Необходимо остановиться подробнее на методике расчета эффективной теплопроводности твердых капиллярно-пористых тел. Для двухфазной системы, твердая фаза которой состоит из двух или более компонентов, может быть рекомендована следующая методика расчета. [12]
Кроме пористости структуры второго порядка т22, для расчета эффективной теплопроводности по формуле ( 3 - 9) необходимо знать теплопроводность Х & компоненты, заполняющей поры структуры второго порядка и теплопроводность Кк самого каркаса. [13]
Напомним, что формула ( 3 - 41) может быть использована не только для расчета эффективной теплопроводности каркаса Як, но и для расчета эффективной теплопроводности всей системы. Выше отмечалось, что формулу ( 3 - 41) целесообразно использовать при анализе теплопроводности зернистых систем с небольшим значением пористости ( т20 5) или для расчета теплопроводности каркаса систем при любой их пористости. [14]
С учетом поправки на зависимость теплопроводности газа от давления и температуры это соотношение широко использовалось для расчета эффективной теплопроводности неметаллических и металлических зернистых и порошкообразных материалов. Результаты расчетов в большинстве случйев удовлетворительно совпадали с экспериментальными данными. [15]
Страницы: 1 2