Расчет - сложный трубопровод
Cтраница 2
Как было видно из предыдущих параграфов, при расчете сложных трубопроводов методом сил появляются весьма обширные системы уравнений, содержащие большое количество неизвестных. Так, расчет трубопровода с двумя узлами и пятью ветвями приводит к системе из 42 уравнений, расчет трубопровода с четырьмя узлами и девятью ветвями - к системе из 78 уравнений. Хотя необходимо при этом отметить, что схема расчета сложного трубопровода методом сил чрезвычайно проста. [16]
 |
Схема сложного кольцевого трубо - ДОИ узловой точки, что провода соответствует первому за. [17] |
Кроме того, кривая потребного напора ЯПОТр необходима для расчета сложного трубопровода с насосной подачей. [18]
Табличную форму задания трубопровода удобно использовать при различного рода машинных методах расчета сложных трубопроводов. [19]
Соотношения ( X-2) и ( X-4) могут быть использованы не только для расчета сложных трубопроводов с параллельными ветвями, но и для расчета сложных трубопроводов с концевой раздачей в тех случаях, когда перепады напоров в ветвях, расходящихся из одного узла, оказываются равными. На рис. X - б показаны некоторые схемы таких трубопроводов. [20]
Соотношения ( 10 - 1) и ( 10 - 2) могут быть использованы не только для расчета сложных трубопроводов с параллельными ветвями, но и для расчета сложных трубопроводов с концевой раздачей в тех случаях, когда потери напора в ветвях, расходящихся из одной узловой точки таких трубопроводов, оказываются равными. На рис. 10 - 6 изображены некоторые схемы таких трубопроводов. [21]
Соотношения ( X-2) и ( X-4) могут быть использованы не только для расчета сложных трубопроводов с параллельными ветвями, но и для расчета сложных трубопроводов с концевой раздачей в тех случаях, когда перепады напоров в ветвях, расходящихся из одного узла, оказываются равными. На рис. X - б показаны некоторые схемы таких трубопроводов. [22]
Большое распространение в машинном расчете трубопроводов получил метод начальных параметров в матричной форме, основы которого изложены в книге [63]: В работе [39] предложен алгоритм расчета сложных трубопроводов с промежуточными пружинными подвесками, реализующий этот метод. Логическая схема алгоритма, основанная на последовательных итерациях, позволяет здесь избежать решения систем линейных алгебраических уравнений высокого порядка. [23]
Повышение потребности в газе, вызывающее расширение газопроводной сети и строительство параллельных ниток газопроводов с целью увеличения их пропускной способности, требует вывода уравнений, необходимых для расчетов сложных трубопроводов. Джонсон и Бервальд ( Johnson and Berwald) [ VII. Вей-маута, в которой коэффициент / был выражен в виде экспоненциальной функции внутреннего диаметра труб. Недавно Смит ( Smith) и его сотрудники [ VII. [24]
Повышение потребности Е Газе, вызывающее расширение газопроводной сети и строительство параллельных ниток газопроводов с целью увеличения их пропускной способности, требует вывода уравнений, необходимых для расчетов сложных трубопроводов. Джонсон и Бервальд ( Johnson and Berwald) [ VII. Вей-маута, в которой коэффициент f был выражен в виде экспоненциальной функции внутреннего диаметра труб. Недавно Смит ( Smith) и его сотрудники [ VII. [25]
Повышение потребности в Газе, вызывающее расширение газопроводной сети и строительство параллельных ниток газопроводов с целью увеличения их пропускной способности, требует вывода уравнений, необходимых для расчетов сложных трубопроводов. Джонсон и Бервальд ( Johnson and Berwald) [ VII. Вей-маута, в которой коэффициент / был выражен в виде экспоненциальной функции внутреннего диаметра труб. Недавно Смит ( Smith) и его сотрудники [ VII. [26]
Соотношения ( 10 - 1) и ( 10 - 2) могут быть использованы не только для расчета сложных трубопроводов с параллельными ветвями, но и для расчета сложных трубопроводов с концевой раздачей в тех случаях, когда потери напора в ветвях, расходящихся из одной узловой точки таких трубопроводов, оказываются равными. На рис. 10 - 6 изображены некоторые схемы таких трубопроводов. [27]
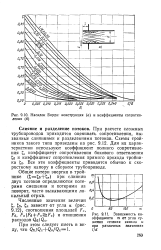 |
Насадок Борда. конструкция ( о и коэффициенты сопротивления ( б.| Зависимость коэффициента т от угла сужения сечения канала при различных значениях Щ. [28] |
При расчете сложных трубопроводов приходится оценивать сопротивления, вызванные слияниями и разделениями потоков. Все эти коэффициенты приводятся обычно к скоростному напору в сборном трубопроводе. [29]
Точность машинных вычислений сочетается с высокой быстротой. Например, расчет сложного трубопровода, состоящего из 130 расчетных участков и имеющего 15 жестких концевых опор и 20 промежуточных, на действие весовых нагрузок и температурного нагрева занимает 1 5 ч ( данные для ЭВМ Минск-2), в то время как расчет такого трубопровода ручным способом представляет собой практически невыполнимую задачу. [30]
Страницы: 1 2 3