Расчет - фильтр
Cтраница 1
Расчет фильтра выполняется следующим образом. Затем оптимизируется полином числителя, чтобы улучшить приближение к заданным характеристикам. [1]
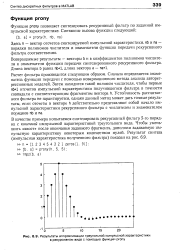 |
Результаты аппроксимации треугольной импульсной характеристики в рекурсивном виде с помощью функции ргопу. [2] |
Расчет фильтра производится следующим образом. Сначала определяется знаменатель функции передачи с помощью ковариационного метода анализа авторегрессионных моделей. Устойчивость рассчитанного фильтра не гарантируется, однако данный метод может дать точные результаты, если отсчеты в векторе h действительно представляют собой начало импульсной характеристики, рекурсивного фильтра с числителем и знаменателем порядков nb и па. [3]
Расчет фильтра производится следующим образом. Сначала рассчитывается импульсная характеристика идеального фильтра Гильберта с заданной групповой задержкой. Затем выполняется аппроксимация этой импульсной характеристики методом разложения соответствующей матрицы Ганкеля по сингулярным числам. [4]
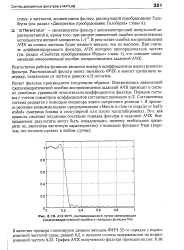 |
АЧХ ФНЧ, синтезированного путем минимизации среднеквадратической ошибки с помощью функции firls. [5] |
Расчет фильтра производится следующим образом. Минимизация взвешенной средиеквадратической ошибки воспроизведения заданной АЧХ приводит к системе линейных уравнений относительно коэффициентов фильтра. Это, как правило, означает неудачное сочетание порядка фильтра и заданной АЧХ. [6]
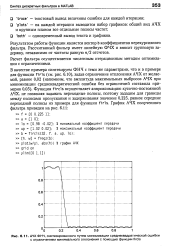 |
АЧХ ФНЧ, синтезированного путем минимизации среднеквадратической ошибки с ограничением минимального отклонения с помощью функции fircls. [7] |
Расчет фильтра осуществляется численным итерационным методом оптимизации с ограничениями. [8]
Расчет фильтров на встречных стержнях с разомкнутыми оконечными линиями отличается от описанного только формулами для вычисления элементов матрицы передачи первого и последнего звена. [9]
Расчет фильтра ведется в два этапа. [10]
 |
Фильтр нижних частот LC. [11] |
Расчет фильтров, изложенный в предшествующих главах, основывался на лестничной цепи без потерь, включенной между генератором и резистивной нагрузкой. Теперь мы снимаем ограничение, чтобы фильтр строился только на реактивных элементах. Мы увидим, что ограниченное число сопротивлений, соответствующим образом введенных в цепь, может привести к более эффективным фильтрам. [12]
Расчет фильтра ведут, исходя из заданного значения SLC и выбранной схемы выпрямления. [13]
Расчет фильтров представляет собой сложную задачу, так как на процесс разделения суспензии оказывает влияние большое число различных факторов. Поэтому ниже дана общая схема расчета фильтров при наличии ряда допущений, упрощающих закономерности разделения суспензий. На практике осаждение твердых частиц нередко предотвращают перемешиванием, а в расчетах принимают средние значения сопротивления фильтровальной перегородки и удельного сопротивления осадка, находимые опытным путем. [14]
Расчет фильтра ведется в следующей последовательности. [15]
Страницы: 1 2 3 4