Расчет - ход - лучая
Cтраница 1
Расчеты тригонометрического хода лучей через мениски с исправленным астигматизмом показали, что в первом случае при переходе от центра поля к краю сферическая аберрация наклонных пучков для бесконечно удаленного предмета не только не растет ( как в случае ближнего расположения зрачка), но даже слегка убывает. Для случая ближнего зрачка приводится формула, выражающая прирост сферической аберрации по полю, но в ней участвует некоторый неопределенный коэффициент А, выражающий степень удаления угла отклонения лучей наклонного пучка от минимума при росте полевого угла. [1]
Так как расчет хода лучей через оптическую систему требует большого объема вычислений, особенно остро стоит вопрос о выборе критерия качества изображения. В принципе, лучевые методы допускают использование любых критериев, в том числе всех описанных в предыдущем параграфе. [2]
Эта зависимость может быть установлена посредством ряда формул, заимствованных нз расчета хода лучей через оптическую систему. [3]
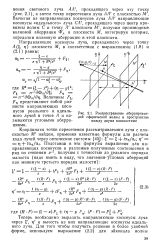 |
Распространение аберрирован. [4] |
Координаты точки пересечения рассматриваемого луча с плоскостью М найдем, применяя известные формулы для расчета хода лучей через оптические системы [45]: g / ссг; f f т ] tan / ccz. Подставив в эти формулы выражения для направляющих косинусов и разложив полученные соотношения в ряд по степеням z - l, получим с точностью до седьмого порядка. [5]
Вычисление их основных параксиальных элементов ( фокусное расстояние, положение главных плоскостей) путем расчета хода лучей через всю систему ввиду большого числа поверхностей представляет задачу, посильную только для ЭВМ, при условии разработки специальных программ. Обычные программы расчета хода лучей через центрированные оптические системы предусматривают ограниченное число поверхностей, обычно не превышающее нескольких десятков. При таких обстоятельствах даже определение положения изображения заданного источника и аберрационных свойств системы превращается в сложную задачу. Однако цикличность процесса вычисления, вызванная повторением оптической схемы через каждые два отражения с одной стороны, и малость отношения воздушного расстояния d к радиусу кривизны зеркал г приводят к тому, что существуют простые и в то же время достаточно точные формулы, позволяющие определить координаты пересечения параксиального луча с поверхностями зеркал и другие важные: характеристики. [6]
Волновая природа света может не приниматься во внимание также и в том случае, когда размеры аберрационного пятна рассеяния в изображении щели, вычисленные из расчета хода лучей, значительно больше размеров центральной дифракционной полосы в идеальном изображении щели. [7]
Значения сумм S, S, SIn, Slcta и SIICft, определяются из условия, что аберрации второй части компенсируют аберрации фронтальной части, которые определяются путем расчета хода лучей. [8]
Когда не хватает условий для определения оптических сил, можно давать некоторым из ннх ряд произвольных значений, которые в дальнейшем уточняются путем интерполирования в зависимости от полученных результатов расчета хода лучей через объектив. [9]
Изложенная методика обладает двумя существенными недостатками: 1) при малом количестве лучей нельзя точно определить контур действующей части поверхности волны; 2) выбор лучей зависит от конфигурации действующей части поверхности волны, которая становится известной лишь после расчета хода лучей, и поэтому необходимо иметь набор интерполяционных формул применительно к различным возможным конфигурациям. [10]
Учитывая изменение высоты ht для различных полевых углов, были вычислены величины поперечной сферической аберрации bgot для линз с измененной толщиной dt вдоль оси при соответственном изменении высоты ht, и для сопоставления эти же величины поперечных аберраций в меридиональной плоскости были вычислены непосредственно путем тригонометричекого расчета хода лучей. [11]
Вычисление их основных параксиальных элементов ( фокусное расстояние, положение главных плоскостей) путем расчета хода лучей через всю систему ввиду большого числа поверхностей представляет задачу, посильную только для ЭВМ, при условии разработки специальных программ. Обычные программы расчета хода лучей через центрированные оптические системы предусматривают ограниченное число поверхностей, обычно не превышающее нескольких десятков. При таких обстоятельствах даже определение положения изображения заданного источника и аберрационных свойств системы превращается в сложную задачу. Однако цикличность процесса вычисления, вызванная повторением оптической схемы через каждые два отражения с одной стороны, и малость отношения воздушного расстояния d к радиусу кривизны зеркал г приводят к тому, что существуют простые и в то же время достаточно точные формулы, позволяющие определить координаты пересечения параксиального луча с поверхностями зеркал и другие важные: характеристики. [12]
Как уже отмечалось, в большинстве случаев расчет оптической системы включает в себя этап численной оптимизации, на котором через различные варианты системы прослеживают ход определенного числа лучей, равномерно заполняющих зрачок, а качество изображения предметной точки оценивают по параметрам диаграммы рассеяния, формируемой этими лучами. Огромная практическая ценность метода расчета хода лучей заключается в том, что он позволяет учитывать полные аберрации системы, а не один-два низших порядка, как методы теории аберраций. Поэтому характеристики системы, полученные расчетом хода лучей, наиболее приближены к реальным. Более того, установленная этим методом работоспособность оптической системы с точки зрения ее аберрационных свойств может быть нарушена при практической реализации объектива только за счет несовершенства его изготовления. [13]
При градуировке однолучевых призменных ИК-спектрометров могут быть использованы различные способы. Первый способ состоит в расчете хода лучей различных длин волн в оптической системе спектрометра. Однако он применяется крайне редко из-за громоздкости и трудоемкости вычислений, а также сравнительно малой точности градуировки. При втором способе градуировки лспользуют эталонные спектры поглощения некоторых веществ, у которых известны положения максимумов отдельных полос. [14]
В ряде случаев при работе со щелями, ширина которых близка к нормальной, и малых аберрациях приходится учитывать волновую природу света. Волновые аберрации, как и поперечные, определяют из расчета хода лучей на ЭВМ. [15]
Страницы: 1 2