Расчет - сложная цепь
Cтраница 2
 |
Смешанное соединение сопротивлений. [16] |
Для расчета сложных цепей существуют различные методы. Наиболее общим из них является применение второго закона Кирхгофа. Этот закон гласит, что во всяком замкнутом контуре алгебраическая сумма эдс равна алгебраической сумме падений напряжений. Необходимо брать алгебраическую сумму потому, что эдс, действующие навстречу друг другу, или падения напряжения, созданные противоположно направленными токами, очевидно, имеют разные знаки. [17]
Для расчета разветвленной сложной цепи, в которой произвольно размещены сопротивления и источники питания, недостаточно применить закон Ома. В этом случае расчетные уравнения, как указывалось выше, составляются по первому ( узловые уравнения) и второму ( контурные уравнения) правилам Кирхгофа. [18]
 |
Мост для измерения сопротивлений. [19] |
Для расчета разветвленной сложной цепи, в которой произвольно размещены сопротивления и источники питания, недостаточно применить закон Ома. [20]
Для расчета разветвленной сложной цепи, в которой произвольно размещены сопротивления и источники питания, недостаточно применить закон Ома. В этом случае расчетные уравнения, как указывалось выше, составляются по первому ( узловые уравнения) и второму ( контурные уравнения) правилам Кирхгофа. [21]
 |
Сложная цепь ( а и ее эквивалентные схемы ( б и ( в. [22] |
При расчете сложных цепей с одним источником ( рис. 3.24, а) целесообразно использовать метод преобразования сложной цепи в простейшую эквивалентную цепь. [23]
При расчете сложной цепи с одним нелинейным элементом цепь следует упростить с помощью метода генератора, эквивалентного линейной части цепи и нагруженного нелинейным элементом. [24]
При расчете сложных цепей с большим числом узловых точек предпочтителен метод контурных токов, который позволяет освободиться от составления уравнений по первому закону Кирхгофа и тем самым значительно сократить общее число совместно решаемых уравнений. [25]
При расчете сложных цепей значительные упрощения вносит метод контурных токов, который является прямым следствием правил Кирхгофа. Сложный контур состоит из системы простых замкнутых контуров. На рис. 194 изображен сложный контур, состоящий из трех простых контуров. В уравнении Кирхгофа при обходе замкнутого контура на каждом его участке между узлами берется сила тока, действительно протекающего по этому участку. На каждом участке контура сила тока, вообще говоря, различна. В методе контурных токов принимается, что на всех участках каждого замкнутого контура течет один и тот же ток. Эти токи называются контурными. Полная сила тока, текущего по участку контура, равна при этом алгебраической сумме сил контурных токов, для которых этот участок является общим. Полный импеданс для каждого участка контура между узлами ( рис. 194) обозначен соответствующим индексом. Положительное направление обхода взято по часовой стрелке. [26]
При расчете сложных цепей с большим числом узловых точек предпочтителен метод контурных токов, который позволяет освободиться от составления уравнений по первому закону Кирхгофа и тем самым значительно сократить общее число совместно решаемых уравнений. [27]
 |
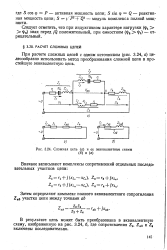
Схема к расчету - елож4в гл. [28] |
При расчете сложных цепей для определения токов во всех ветвях цепи необходимо знать сопротивления ветвей, а также значение и направление всех эдс. [29]
При расчете сложных цепей с одним источником ( рис. 2.25, а) целесообразно использовать метод преобразования сложной цепи в простейшую эквивалентную цепь. [30]
Страницы: 1 2 3 4 5