Расчет - воспроизводимость
Cтраница 1
Расчет воспроизводимости не вызывает затруднений. Значительно труднее решается вопрос о правильности результатов. Очень часто при параллельных анализах наблюдается хорошая сходимость; однако та же серия образцов в другой лаборатории, а иногда даже у другого химика дает результаты, также сходящиеся между собой, но отличающиеся от первых. [1]
Это уравнение точнее, так как в знаменателе подкоренного выражения стоит п - 1, что делает невозможным расчет воспроизводимости на реновации одного опыта. Кроме того, при возведении в квадрат отрицательные значения отклонений становятся положительными. [2]
Это уравнение точнее, так как в знаменателе подкоренного выражения стоит п - 1, что делает невозможным расчет воспроизводимости на основании одного опыта. Кроме того, при возведении в квадрат отрицательные значения отклонений становятся положительными. [3]
Среднее отклонение от среднего результата характеризует воспроизводимость. Для расчета воспроизводимости в большинстве случаев достаточно применить следующий простой способ. Очевидно, что всякая ошибка - и положительная и отрицательная - характеризует отклонение. Поэтому для расчета отбрасывают знаки отклонений. [4]
Однако присутствие хрома неизбежно приведет к систематической ошибке при установлении содержания алюминия и к еще более серьезной ошибке при дальнейшем технологическом процессе. Эта ошибка не исправляется расчетом воспроизводимости, между тем химик -, помнящий Качественный анализ, всегда сможет обнаружить и исправить подобную ошибку. [5]
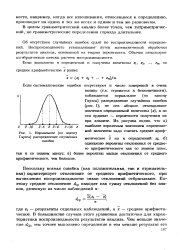 |
Нормальное ( по закону. [6] |
Воспроизводимость устанавливают путем математической обработки результатов анализа, основанной на теории вероятности. Обычно используют апгебраические методы расчета воспроизводимости. [7]
Воспроизводимость устанавливают путем математической обработки результатов анализа, основанной на теории вероятности. Обычно используют алгебраические методы расчета воспроизводимости. [8]
Кроме различия между понятиями правильности и воспроизводимости, необходимо иметь в виду следующее. Воспроизводимость устанавливается путем математической обработки результатов. Ниже рассмотрены основные вопросы, связанные с расчетом воспроизводимости. Расчет основан главным образом на теории вероятностей. Поэтому средний результат принимают за правильный. Однако этот прием условный и относится только к расчету воспроизводимости. Правильность же результатов химического анализа не может быть установлена никакой математической обработкой конечных результатов. Методы установления правильности рассмотрены отдельно в этом же параграфе. [9]
Численные значения, рассчитанные по уравнениям ( 2) и ( 3), в общем близки. Физический смысл операций, предложенных в уравнении ( 3), следующий. В знаменателе подкоренного выражения уравнения ( 3) стоит ( п - 1) для того, чтобы сделать невозможным расчет воспроизводимости на основании только одного опыта: в этом случае п - 1 0, и квадратичная ошибка будет равна бесконечности. [10]
Два разных метода редко могут давать результаты с одинаковой ошибкой. Поэтому сходимость результатов двух ( или более) разных методов указывает на их правильность. В этих случаях необходимо использовать правила расчета воспроизводимости. Метод может считаться правильным, если его воспроизводимость характеризуется цифрами того же порядка, что и различие среднего арифметического значения, полученного каждым из методов. [11]
Кроме различия между понятиями правильности и воспроизводимости, необходимо иметь в виду следующее. Воспроизводимость устанавливается путем математической обработки результатов. Ниже рассмотрены основные вопросы, связанные с расчетом воспроизводимости. Расчет основан главным образом на теории вероятностей. Поэтому средний результат принимают за правильный. Однако этот прием условный и относится только к расчету воспроизводимости. Правильность же результатов химического анализа не может быть установлена никакой математической обработкой конечных результатов. Методы установления правильности рассмотрены отдельно в этом же параграфе. [12]
Страницы: 1