Расчет - четырехполюсник
Cтраница 2
Формулы (2.16) - (2.19) являются инвариантными по отношению к любой системе параметров, и поэтому простой заменой в них символов получим необходимые соотношения для расчета идеализированного четырехполюсника, описываемого Z, iG или Я-пара-метрами. [16]
Современный канал связи большой протяженности представляет собой каскадное соединение десятков, а иногда и сотен четырехполюсников. Расчет четырехполюсников на стадии проектирования ведут таким образом, чтобы все четырехполюсники, составляющие канал, были соединены друг с другом по принципу согласованности характеристических сопротивлений. Такое соединение облегчает расчет характеристических параметров канала связи в целом ( рассматриваемого как четырехполюсник), а с энергетической точки зрения позволяет свести к минимуму потерю мощности сигнала в четырехполюсниках канала связи. [17]
Матрица (8.9) называется также цепочечной матрицей четырехполюсника. Методы расчета четырехполюсников с помощью матричных уравнений (8.3) и (8.7) - (8.12)) называются матричными методами. При составлении уравнений (8.9) - (8.12) находят уравнения связи между основными параметрами четырехполюсника. [18]
Если он является симметричным ( хотя соединяемые четырехполюсники могут быть несимметричными), то по формулам (8.69) определяют параметры соответствующих канонических схем, по которым опять-таки можно анализировать их свойства и производить необходимые расчеты. Описанная процедура расчета четырехполюсников называется методом характеристических параметров. [19]
 |
Бисекция произвольного симметричного четырехполюсника. [20] |
Характеристическими параметрами четырехполюсника называют его входные сопротивления и передаточные функции в режиме двустороннего согласования четырехполюсника с нагрузочными сопротивлениями по полной мощности. Использование этих параметров в некоторых случаях существенно упрощает анализ и расчет четырехполюсников. [21]
В устройствах связи многие цепи используются в качестве четырехполюсников. Некоторые их общие свойства можно изучать безотносительно к схемам конкретных цепей. Существуют специфические методы анализа общих свойств и общие методы расчета четырехполюсников с произвольной схемой. Такие методы рассматриваются в настоящей главе. [22]
 |
Эквивалентные схемы ре - [ IMAGE ] Эквивалентные схемы ре. [23] |
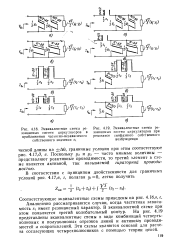
Соответствующие эквивалентные схемы приведены на рис. 4.18 е, г. Аналогично рассматриваются случаи, когда частотная зависимость si имеет резонансный характер. В эквивалентной схеме при этом появляется третий колебательный контур. На рис. 4.19 представлены эквивалентные схемы в виде комбинаций четвертьволновых и полуволновых отрезков линий и активных проводи-мостей и сопротивлений. Эти схемы являются основой для расчета согласующих четырехполюсников с помощью теории цепей. [24]
Страницы: 1 2