Расчет - энергия - кристаллическая решетка
Cтраница 2
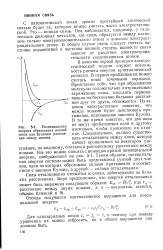 |
Потенциальная энергия образования ионной связи как функция расстояния между ионами. [16] |
В качестве первой проверки электростатической модели служит возможность расчета энергии кристаллической решетки. В первом приближении можно считать ионы точечными зарядами. Представим себе, что при образовании молекулы положительно и отрицательно заряженные ионы, находясь первоначально на бесконечно большом расстоянии друг от друга, сближаются. Из законов электростатики известно, что между ионами будет действовать притяжение, описываемое законом Кулона. В то же время известно, что два иона не могут приблизиться один к другому настолько, чтобы произошло их слияние. Следовательно, должно существовать отталкивание между ними, которое начнет проявляться на некотором расстоянии, по-видимому, близком к равновесному расстоянию между ионами. Таким образом, потенциальная энергия системы может быть представлена суммой двух членов, один из которых обусловлен силами притяжения в соответствии с законом Кулона, а другой - силами отталкивания. [17]
Проверкой теории ионной связи, которая базируется на электростатической модели, служит расчет энергии кристаллической решетки. [18]
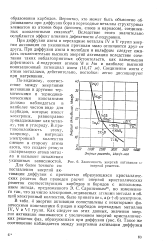 |
Зависимость энергий активации от энергий решеток. [19] |
Для более точного сопоставления энергий активации диффузии с прочностью образующихся кристаллических решеток был проведен расчет энергий кристаллических решеток соответствующих карбидов и боридов с использованием метода, предложенного Саркисовым16, но измененного так, что за число электронов, отдаваемых атомами металла в общий электронный коллектив, было принято не s, a ( s - f - d) электронов. [20]
Сопоставление уравнения (111.87) для расчета энергии связи в ионной молекуле и уравнения (IV.13) для расчета энергии кристаллической решетки показывает, что если пренебречь сравнительно небольшим изменением г0 при переходе газообразных молекул в кристалл, то можно считать, что энергия образования кристалла из ионов в а раз превышает энергию образования соответствующего числа ионных молекул. Как видно из табл. 24, коэффициенты Маделунга больше единицы. Поэтому ионные кристаллы имеют высокие температуры плавления и большие теплоты сублимации. [21]
Отметим здесь также и другие работы, в которых были сделаны попытки глубже проникнуть в основы расчета энергии кристаллической решетки. [22]
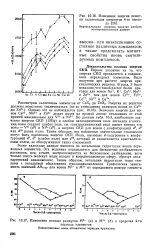 |
Изменение энергии решетки галогенидов элементов 4-го периода [ 261. [23] |
Первое указание на то, что энергия СКП проявляется в соединениях переходных элементов, было получено при расчете энергии кристаллических решеток. [24]
Первому из этих аспектов в настоящее время уделяется сравнительно мало внимания, хотя в принципе вопросы упаковки комплексов в кристалле имеют первостепенное значение для расчета энергии кристаллической решетки, а значит, и для получения фундаментальных параметров, входящих во все термодинамические соотношения. [25]
Существенным недостатком теории Аррениуса является и то, что она не указывает причин, вызывающих ионизацию электролитов в растворах. Расчеты энергии кристаллической решетки AGP, разрушение которой должно предшествовать появлению свободных ионов, присутствующих в растворе, показывают, что количество термической энергии при обычных температурах слишком мало по сравнению с тем, оторое надо затратить на разрушение решетки. [26]
Существенным недостатком теории Аррениуса является и то, что она не указывает причин, вызываощих ионизацию электролитов в растворах. Расчеты энергии кристаллической решетки AGP, разрушение которой должно предшествовать появлению свободных ионов, присутствующих в растворе, показывают, что количество термической энергии при обычных температурах слишком мало по сравнению с тем, которое надо затратить на разрушение решетки. [27]
Дополнительным подтверждением правомерности ионных моделей служит, по мнению этих ученых, обычно вполне удовлетворительное совпадение величин энергии кристаллических решеток, полученных из цикла Борна - Габера или рассчитанных по формуле Борна ( 3), основанной на представлениях чисто ионной связи. Например, расчет энергии кристаллической решетки хлорида натрия по формуле Борна дал величину 180 ккал / моль, а экспериментальная величина из цикла Борна - Габера составляет 186 ккал / моль. [28]
Остановимся более подробно на электростатических моделях. Основными областями их применения являются расчеты энергий кристаллических решеток солей, энергий комплексообразования в газовой фазе и растворах и энергий гидратации. [29]
Циклы, изображенные на рис. II, 2, дают возможность вычислить теплоты любых входящих в них процессов. Так, цикл, изображенный слева, который называется циклом Борна-Хабера, используется для расчета энергии кристаллической решетки. Так называется энергия, поглощаемая при разрушении одного моля кристаллического вещества с образованием газообразных одноатомных ионов, удаленных друг от друга ( идеальный газ), или убыль энергии при обратной реакции. [30]
Страницы: 1 2 3