Расчет - упругопластическая деформация
Cтраница 1
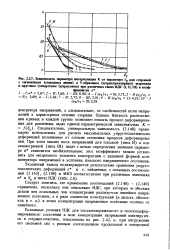
Расчет упругопластических деформаций для изотермического малоциклового нагружения с помощью данной модели упрощается, так как используется одна статическая диаграмма деформирования для температуры t процесса нагружения. [1]
Для совершенствования и развития приближенных методов расчета упругопластических деформаций соотношение Нейбера модифицировано путем введения поправочных функций и корректирующих показателей при основных параметрах. [3]
Следовательно, универсальную зависимость (2.148) правомерно использовать для расчета максимальных упругопластических деформаций независимо от степени стеснения процесса деформирования. При этом анализ поля напряжений для плоской ( типа II) и осе-симметричной ( типа III) задач с целью определения значения параметра а становится необязательным: этот коэффициент можно установить для модельного элемента конструкции с заданной формой концентратора напряжений в условиях плоского напряженного состояния. [5]
Следовательно, универсальную зависимость (2.148) правомерно использовать для расчета максимальных упругопластических деформаций независимо от степени стеснения процесса деформирования. При этом анализ поля напряжений для плоской ( типа И) и осе-симметричной ( типа III) задач с целью определения значения параметра а становится необязательным: этот коэффициент можно установить для модельного элемента конструкции с заданной формой концентратора напряжений в условиях плоского напряженного состояния. [7]
Последнее обстоятельство свидетельствует о возможности использования единой зависимости А, - ев относительных координатах для расчета упругопластической деформации металлических рукавов различных типоразмеров. [8]
Таким образом, введение показателя п в уравнение (2.130) приводит к существенному повышению точности приближенного метода расчета упругопластических деформаций в зонах концентрации напряжений элементов конструкций. [10]
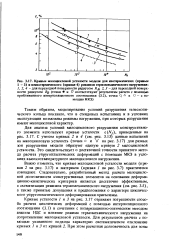 |
Кривые малоцикловой усталости модели для изотермических ( кривые 1 - 3 и неизотермического ( кривая 4 режимов термомеханического нагружения. [11] |
Для анализа условий малоциклового разрушения конструктивного элемента используют кривые усталости е ( ЛМ, приведенные на рис. 3.17. С учетом кривых 2 и 4 ( см. рис. 3.13) данные испытаний на малоцикловую усталость ( точки о и V на рис. 3.17) для разных зон разрушения модели образуют единую кривую 2 малоцикловой усталости. Это свидетельствует о достаточной точности принятого метода расчета упругопластических деформаций с помощью МКЭ в условиях высокотемпературного малоциклового нагружения. [12]
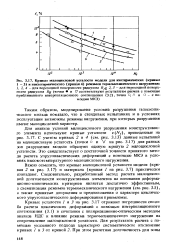 |
Кривые малоцикловой усталости модели для изотермических ( кривые 1 - 3 и неизотермического ( кривая 4 режимов термомеханического нагружения. [13] |
Для анализа условий малоциклового разрушения конструктивного элемента используют кривые усталости e ( Nt), приведенные на рис, 3.17. С учетом кривых 2 и 4 ( см. рис. 3.13) данные испытаний на малоцикловую усталость ( точки о и V на рис. 3.17) для разных зон разрушения модели образуют единую кривую 2 малоцикловой усталости. Это свидетельствует о достаточной точности принятого метода расчета упругопластических деформаций с помощью МКЭ в условиях высокотемпературного малоциклового нагружения. [14]
Наиболее часто встречающейся проблемой, возникающей при использовании эйлерова представления, является численная диффузия. Она обусловлена тем, что при эйлеровом описании поверхности раздела в течении не могут быть локализованы с точностью, большей размера одной ячейки, если не вводить дополнительные степени свободы в этом представлении. Численная диффузия проявляется как преждевременное смешение среды на протяжении всей расчетной ячейки, что приводит к размытию контактных границ. Проблемы возникают также при расчете упругопластических деформаций и релаксационных явлений, где необходимо помнить предысторию процесса в каждой материальной частице. [15]
Страницы: 1 2