Аккуратный расчет

Cтраница 1

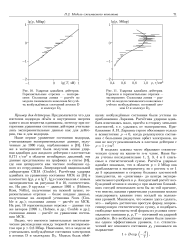
Зависимость постоянной затухания плазмы вблизи п нескольких значениях v / ю. [1]

Аккуратный расчет показывает, однако, что переход от полной непрозрачности плазмы к пропусканию излучения вблизи пе - крит делается менее резким. [2]

Первый аккуратный расчет соггО) был выполнен только в 1979 г. Панга-ли, Рао и Берном [19] методом МК. В ячейке при плотности 1 г / см3 кТ 283 К содержалось 214 молекул воды с потенциалом ST2 ( так называемая вода Стиллинджера, впервые применившего этот потенциал в исследовании ее свойств методом МД [20]) и две леннард-джонсовские частицы. Параметры потенциалов были выбраны следующими: ст12 0 343 нм, е12 / к 77 82К, а22 0 412 нм, е22 / / г: 170 1 К, потенциалы обрезались на сфере при г 0 846 нм. [3]

Более аккуратный расчет дает вместо коэффициента 3 величину тг2 / 2, что не сильно отличается от нашей оценки. Существенным моментом в полученной формуле для электронной теплоемкости является то, что при Т 0 она составляет порядка процента от решеточной теплоемкости, но в силу ее линейной зависимости от температуры в области низких температур она может стать доминирующей. Обычно решеточная и электронная теплоемкости сравниваются при температуре в несколько Кельвинов. [4]

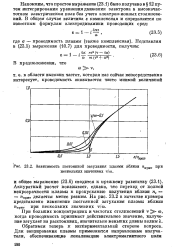
Проекции электронных траекторий на плоскость г, 9 для потоков с частично экранированным катодом ( К 0. [5]

Эти преимущества оправдывают более сложный по сравнению с бриллюэновским случаем расчет таких систем и более высокие магнитные поля. В аккуратных расчетах приходится также учитывать неламинарность потока и неравномерное распределение плотности тока по сечению пучка. [6]

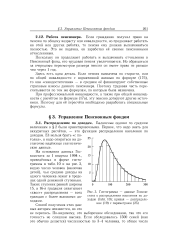Гистограмма - данные Госкомстата о распределении населения по доходам ( 10. кривая - распределение ( 19 с параметрами ( 25. [7]

Первое, что надо знать для аккуратных расчетов, - это функция распределения населения по доходам. [8]

Формулы (8.1) - (8.3) носят, конечно, лишь оценочный характер. При фактическом сравнении экспериментальных и теоретических данных необходим более аккуратный расчет. [9]

Характерной особенностью большинства задач, встречающихся в приложениях, является нерегулярность границ рассматриваемых областей. К тому же на линиях излома обтекаемых идеальным газом поверхностей возникают пучки волн разрежения, аккуратный расчет которых невозможен без использования разностных сеток, адаптированных к каждому излому. Последнее вместе со сложностью рассчитываемых областей приводит к необходимости вести счет на существенно нерегулярных сетках. С другой стороны, широко распространенные разностные схемы, как правило, обеспечивают аппроксимацию уравнений течения только на достаточно хороших сетках, не имеющих изломов сеточных линий и линий скачкообразного изменения размеров разностных ячеек. Отмеченные обстоятельства делают актуальной задачу построения схем, обеспечивающих хотя бы с первым порядком аппроксимацию уравнений течения на произвольных сетках. [10]

Заметим, что на процессах отражения могут сказаться эффекты поляризации, которыми мы здесь до сих пор пренебрегали. Отметим, наконец, что кроме отраженного излучения небольшой вклад в значения / х ( 0, nt) может вносить излучение, рассеянное толщей воды, аккуратный расчет которого, однако, весьма затруднителен. [11]

Ударная адиабата дейтерия. Горизонтальные отрезки - эксперимент. Сплошная линия - расчет по модели сжимаемого коволюма без учета возбужденных состояний атомов D и молекул D2.| Ударная адиабата дейтерия. Кружки и горизонтальные отрезки - эксперимент. Сплошная линия - расчет по модели сжимаемого коволюма с учетом возбужденных состояний атомов D и молекул D2. [12]

В моделях плазмы часто обрывают статистическую сумму на каком-то n - м члене. Нами были учтены последовательно 1, 2, 3, 4 и 5 слагаемых в статистической сумме. Аккуратный расчет возбуждений атомов и молекул при наличии ближайших соседей невозможен хотя бы по той причине, что неясно, какими граничными условиями можно моделировать влияние этих соседей на положения уровней. [13]

Наконец, на нижней границе льда г - ( AS A /) разность потоков тепла во льду и в воде ( второй из них должен определяться при помощи уравнений динамики океана) определяет HWi, а потому и значение Ewi, дающее в водном эквиваленте скорость намерзания или стаивания льда снизу. Отметим, что аккуратный расчет упомянутого здесь потока тепла в воде ( направленного из воды вверх в лед) требует учета солености воды, изменений толщины и других характеристик ВПС и его взаимодействия с более глубокими слоями океана; так, при намерзании льда снизу выделение соли увеличивает плотность воды в ВПС и создает возможность развития конвекции. [14]

Наконец, на нижней границе льда г - ( AS A /) разность потоков тепла во льду и в воде ( второй из них должен определяться при помощи уравнений динамики океана) определяет HWi, а потому и значение EWi, дающее в водном эквиваленте скорость намерзания или стаивания льда снизу. Отметим, что аккуратный расчет упомянутого здесь потока тепла в воде ( направленного из воды вверх в лед) требует учета солености воды, изменений толщины и других характеристик ВПС и его взаимодействия с более глубокими слоями океана; так, при намерзании льда снизу выделение соли увеличивает плотность воды в ВПС и создает возможность развития конвекции. [15]

Страницы: 1 2