Расширение - отверстие
Cтраница 2
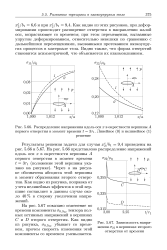
Аналогично может быть рассмотрена задача о расширении сферического отверстия в грунте, деформирование которого подчиняется той же схеме. [16]
Как видно из этих рисунков, при деформировании происходит расширение отверстия в направлении малой оси, возрастающее со временем; при этом перемещения, вызванные упругим деформированием, относительно невелики по сравнению с дальнейшими перемещениями, вызванными протеканием вязкоупру-гих процессов в материале тела. Видно также, что форма отверстий становится асимметричной, что объясняется их взаимовлиянием. [18]
 |
Схема к расчету толщины пленки. [19] |
По возникшему периметру образуются наплывы, толщина которых увеличивается по мере расширения отверстия. По размерам наплывов, образующихся при разрушении пленок, сделана попытка оценить ее толщину. [20]
Для второй группы работ применяются зенкеры: 1) с цапфой для расширения отверстий под головку винтов ( цилиндрической формы); 2) с цапфой для расширения отверстий под шейку винтов. [21]
 |
Укрепление перегородок с помощью болтов. [22] |
Наконец, появление коррозии с обеих сторон может вызвать быстрое разъедание и расширение отверстий, а следовательно, и снижение плотности. [23]
Центральная зона зенкера не может производить резания и поэтому зенкеры применяют только для расширения отверстий. [24]
Численное интегрирование уравнения (2.4.110) требует знания производной г / 0 в начальный момент расширения отверстия, вычисление которой сводится к дифференцированию уравнения (2.4.110) и подстановке начальных значений параметров. [25]
 |
Инструменты для сверления п развертывания отверстий. а - перовое сверло. б - спиральное сверло. в - развертки. г - зенкер. [26] |
К числу разверток относятся также зенкеры ( рис. 161 г), служащие для расширения отверстий на конус для головок потайных шурупов и винтов. [27]
Цилиндрические зенкеры применяют для зенкования цилиндрических потаев или торцевания поверхности изделия возле отверстия, а также для расширения отверстий. [28]
Согласно гидродинамической теории, в процессе пробивания преграды струей преграда раздвигается так, что все ее элементы получают скорости, соответствующие расширению отверстия; струя при этом размазывается по стенкам. Мы считаем процесс законченным, когда вся струя размажется. На самом деле в схеме идеальной жидкости полученное жидкостью движение будет продолжаться так, что диаметр отверстия будет неограниченно расти. Задача определения диаметра отверстия, таким образом, в схеме идеальной жидкости неразрешима. Начальное распределение скоростей можно брать из схемы идеальной жидкости ( или газа), а дальнейший счет нужно вести в вязко-упругой среде. [29]
В момент полного прохождения тела через срединную поверхность давление в отверстии исчезает и справедливо уравнение ( 2.4.110), для которого начальным значением является скорость расширения отверстия в этот момент. [30]
Страницы: 1 2 3 4