Значение - среднеквадратического отклонение
Cтраница 1
Значение среднеквадратического отклонения позволяет судить о точности результата измерений, а систематическая погрешность о правильности его. [1]
Одной из наиболее важных характеристик вариации является значение среднеквадратического отклонения, обычно обозначаемое s или ст. Основное достоинство среднеквадратического отклонения состоит в том, что его можно рассчитать с помощью объективной математической формулы, а не путем оценочных методов, как в случае с межквартильным размахом. [2]
Количество сверхурочных часов - это переменная, обозначаемая х, для которой мы хотим найти значение среднеквадратического отклонения. [3]
Значения дисперсии могут быть объединены напрямую, а значения среднеквадратического отклонения - нет. [4]
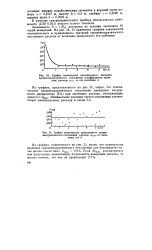
Зависимость G ( GK) построена по средним значениям 16 серий измерений. На рис. 34, 35 приведены графики зависимости относительного и приведенного значений среднеквадратического отклонения расхода от величины измеряемого его значения. [6]
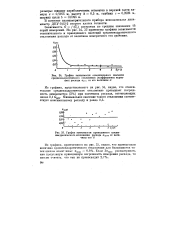 |
График зависимости относительного значения среднеквадратического отклонения ( коэффициента вариации расхода оь от его величины G.| График зависимости приведенного средне. [7] |
Зависимость G - f ( GK) построена по средним значениям 1Ь серий измерений. На рис. 34, 35 приведены графики зависимости относительного и приведенного значений среднеквадратического отклонения расхода от величины измеряемого его значения. [8]
Если их расхождение сохраняется большим, превышающим еа, то управляющее устройство 20 подает команду на увеличение длительности измерения еше на один интервал А. Так будет происходить до тех пор, пока среднеквадратическое отклонение за интервал t n & t будет равным ( с точностью до ест) содержащемуся в блоке 18 среднеквадратическому отклонению за t ( п - 1) Af. Равенство этих величин будет свидетельствовать о том, что вычисленное в результате испытания значение среднеквадратического отклонения имеет установившееся значение. [9]
Если их расхождение сохраняется большим, превышающим еа, то управляющее устройство 20 подает команду на увеличение длительности измерения еше на один интервал А. Равенство этих величин будет свидетельствовать о том, что вычисленное в результате испытания значение среднеквадратического отклонения имеет установившееся значение. [10]
Переходы системы с одного уровня на другой определяются сменой действующих факторов, оказывающих на каком-то этапе превалирующее влияние на процесс. Идентификация модели осуществляется следующим образом: по исходному информационному массиву определяются коэффициенты модели, и вычисляется среднеквадратическое отклонение. При поступлении последующей информации коэффициенты модели и среднеквадратическое отклонение заново пересчитываются. При наблюдении скачка в значениях среднеквадратического отклонения считается, что система перешла на новый качественный уровень. [11]
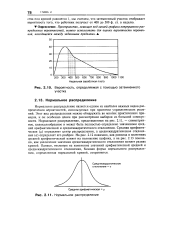 |
Вероятность, определяемая с помощью затемненного участка. [12] |
Нормальное распределение является одним из наиболее важных видов распределения вероятностей, используемых при принятии управленческих решений. Этот вид распределения можно обнаружить во многих практических примерах, и он особенно ценен при рассмотрении выборок из большой совокупности. Нормальное распределение, представленное на рис. 2.11, - симметричное, колоколообразное и может быть полностью определено значениями средней арифметической и среднеквадратического отклонения. Средняя арифметическая ( ц) определяет центр распределения, а среднеквадратическое отклонение ( ст) определяет его разброс. На рис. 2.12 показано, как разница в значениях средней арифметической влияет на положение графика, а на рис. 2.13 показано, как увеличение значения среднеквадратического отклонения меняет размах кривой. Однако, несмотря на изменение значений арифметической средней и среднеквадратического отклонения, базовая форма нормального распределения, определенная нормальной кривой, сохраняется. [13]
Часто такого рода базовый анализ данных обеспечивает достаточное количество информации для составления внутренних циркуляров, хозяйственных отчетов и открытых материалов. К двум наиболее важным методам обобщения данных относится расчет средней и меры вариации. Средние можно рассчитывать по-разному, но наиболее часто используются значения арифметической средней, медианы и моды. Аналогично, имеется несколько показателей вариации, которые можно использовать. Сюда относятся такие два значимых показателя, как значения среднеквадратического отклонения и квартилей. [14]
Страницы: 1