Реактор - идеальное смешение
Cтраница 3
При расчете реактора идеального смешения надо задаться температурой реакции и, решив систему уравнений типа ( V. [31]
Математическое описание реактора идеального смешения для различных типов реакций приведено в главе II ( см. стр. Здесь использованы некоторые из результатов, полученных выше, для постановки и решения оптимальных задач с указанными реакторами. [32]
Физическим аналогом реактора идеального смешения является реактор, в котором установлена развитая изотропная турбулентность с очень большими значениями пульсационных скоростей. [33]
Для каскада реакторов идеального смешения, в котором проводится реакция первого порядка, протекающая без изменения числа молей реагирующих веществ, определить выигрыш в суммарном реакционном объеме каскада по сравнению с одиночным реактором идеального смешения, рассчитанным на ту же степень превращения исходного реагента А. [34]
При рассмотрении реакторов идеального смешения предполагается, что в аппарате имеет место равномерное распределение молекул всех реагирующих веществ. При реальных же условиях перемешивания [32] могут возникать такие ситуации, когда равномерно распределены не молекулы реагирующих веществ, а элементы объема различного состава. Размер этих элементов может быть ничтожно мал по сравнению с размерами аппарата, но велик по сравнению с размерами молекул. [35]
Управление работой реактора идеального смешения - следующее важное изменение, внесенное в систему управления работой установки, - также нуждается в том, чтобы его прокомментировать. [36]
Ограничимся рассмотрением реакторов идеального смешения, для которых математические модели сводятся к системам обыкновенных дифференциальных уравнений. Реакторы, модели которых составляются в настоящей главе, различаются по типу массопередачи, условиям теплообмена и кинетике реакций. [37]
Два проточных реактора идеального смешения различных размеров соединены последовательно. [38]
Это свойственна реакторам идеального смешения. [39]
Применительно к реакторам идеального смешения при использовании типовых моделей статические характеристики определяют по табл. 3 где приведены формулы вычисления основных характеристик X в случае микросмешения. Уравнения решают последовательно для каждого к-го реактора ( от к1 до кЫ) по следующей схеме. Находят концентрации мономера из уравнения n - й степени ( п2, или 3, или 5, в зависимости от типа обрыва), затем находят концентрации активных цепей единичной длины и моментов активных цепей в порядке увеличения их номера ( нулевой, первый, второй... Далее находят моменты неактивных цепей в порядке увеличения их номера. Размерность вектора основных координат X применительно к типовым модулям ограничена восемью, но при необходимости число координат может быть увеличено. [40]
 |
Схема реакторов Берти. [41] |
Мешалка в реакторах идеального смешения может быть размещена как внутри, так и вне реакционного объема. [42]
Наиболее широко используются реакторы идеального смешения В этих реакторах перемешивание реакционной смеси может прош водиться мешалками или пузырьками пара в случае проведения СИЕ теза при кипении содержимого реактора. [43]
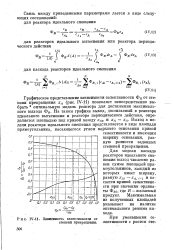 |
Зависимость селективности от ПРИ уменьшении се-степени превращения, лективности с ростом сте. [44] |
Для модели каскада реакторов идеального смешения выход численно равен сумме площадей прямоугольников, каждый из которых имеет ширину, равную хм - ХА - х и касается кривой селективности при значении ординаты ФЛ1, где R - желаемый продукт. Максимальная из полученных площадей указывает на наличие оптимального режима выхода. [45]
Страницы: 1 2 3 4