Значение - параметр - связь
Cтраница 1
Значения параметров связи с базой данных необязательно хранить в текстовом файле; их можно задать непосредственно. Однако, лучше хранить их в текстовом файле, поскольку при изменении значения достаточно будет изменить лишь текстовый файл. [1]
Эти значения параметра связи в начале и конце поддиапазона принимают для последующих расчетов. [2]
Устанавливаются значения параметра симметрической связи ( - I) 1 для отражений hkj; их сумма определяет соотношение между знаками двух сопоставляемых отражений. [3]
Если не задается значение параметра связи, назначается лишь его оценка, и подсистемы сами определяют величину этого параметра, то методы, использующие этот принцип, называют методами неявной декомпозиции, или методами цен. В противном случае, когда непосредственно задаются значения переменных связи, подобные методы называются методами явной декомпозиции. [4]
Ренормировка возможна, пока значения параметра связи достаточно малы. [5]
В методе явной декомпозиции в качестве переменных координации используются значения параметра связи между подсистемами, разрываемые в процессе декомпозиции. [6]
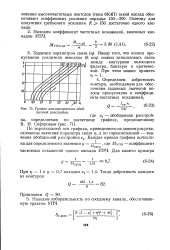 |
График для определения обоб. [7] |
По вертикальной оси графика, приведенного на данном рисунке, отложены значения параметра связи т ], а по горизонтальной - значения обобщенной расстройкихг. [8]
В методе явной декомпозиции, или, как его часто называют, методе закрепления переменных, в качестве переменных координации используются значения параметров связи между подсистемами, разрываемыми в процессе декомпозиции. При этом общая задача оптимизации ХТС разбивается на ряд локальных задач для каждой из подсистем и задачу координации, заключающуюся в выборе таких значений переменных координации, при которых глобальная целевая функция достигает максимума. [9]
Х-23 - l t) 2 - 1 расположены симметрично относительно точки резонанса и характеризуют максимум двугорбой кривой. В зависимости от значения параметра связи тс эти корни имеют вещественное или мнимое значение. Рассмотрим три возможных случая. [10]
Используя методику пункта 6 разд. II настоящего параграфа, выбирают значения параметра связи для конца т) и начала т ] а поддиапазона. [11]
Численные коэффициенты в формулах соответствуют значениям параметра связи или относительной расстройке между контурами от 0 6 до 3 0, обычно имеющим место в реальных схемах частотных детекторов. [12]
Декомпозиционные методы оптимизации делятся на два больших класса: методы неявной и явной декомпозиции. Если значение параметра связи не задается, а лишь назначается его оценка, и подзадачи сами определяют значение этого параметра, то методы, использующие этот принцип, являются методами неявной декомпозиции, или методами цен. В противном случае, когда непосредственно задаются значения переменных связи, подобные методы являются методами явной декомпозиции. [13]
 |
Резонансные кривые свя эанных контуров. [14] |
Из рис. 4 - 6 следует, что при увеличении параметра связи боковые ветви резонансной кривой двух связанных контуров делаются более крутыми и она становится более похожей на прямоугольник. Но при параметре связи П1 резонансная кривая связанных контуров становится двугорбой и провал в ней увеличивается с ростом ц, что приводит к значительному отклонению от желаемой прямоугольной формы. Кроме того, при двугорбой форме резонансной кривой настройка контуров более трудна, чем при одногорбой, так как в этом случае нельзя каждый контур настраивать по максимуму напряжения на нем. Поэтому в радиовещательных приемниках редко берут связь больше критической. Каждому значению параметра связи будет соответствовать своя кривая. На рис. 4 - 4 приведены обобщенные резонансные кривые двухконтурных фильтров. Из сопоставления их с обобщенной кривой одиночного контура следует, что за пределами полосы пропускания они идут более круто. Следовательно, полосовые фильтры обеспечивают лучшее соотношение между шириной полосы пропускания и избирательностью, что и является их большим преимуществом. [15]
Страницы: 1