Значение - параметр - форма
Cтраница 1
Значения параметра формы р найдены методом последовательного приближения путем линеаризации графиков. Для рассматриваемых данных при р 1 и р 5 получаем кривые с противоположной кривизной, а значению р 3 соответствует приближенно линейный график. [1]
При указанных выше значениях параметра формы теория Рейсснера удовлетворительно предсказывает величину критической нагрузки, а теория Миндлина - частоты собственных колебаний. Однако ни одна из них не позволяет достаточно точно определить соответствующее напряженное состояние. [2]
При интерполяции параметров оператор создает опорные кадры на языке значений параметров формы объектов, затем параметры интерполируются с некоторым шагом. На каждом шаге приращения строится свое изображение. [3]
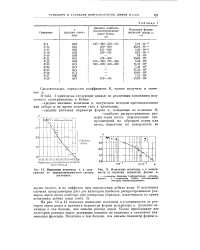 |
Изменение величины п в зависимости от гранулометрического состава песчаника. [4] |
На рис. 13 и 14 показано изменение величины п в зависимости от размеров зерен песка и значения параметра формы резервуара и. [5]
Как и следовало ожидать, анализ чувствительности при выборе плана испытаний на основе кривых риска по существу представляет повторение процесса выбора для нескольких значений параметра формы. На основе таких повторных выборов можно определить, каким образом изменяется стоимость испытаний в зависимости от выбранного параметра. Если стоимость нечувствительна к изменениям значения параметра формы, то в процессе выбора плана испытаний можно ограничиться грубой его оценкой. Однако если стоимость испытаний чувствительна к значению этого параметра, то следует приложить дополнительные усилия для получения разумных оценок параметра формы или воспользоваться более дорогими методами непараметрических испытаний. [6]
Если выбор плана испытаний производится на основе рабочих характеристик или риска производителя - потребителя, то анализ сводится к определению влияния на выбор плана раз - - личных значений параметра формы. Однако анализ следует выполнять на основе фактической надежности, а не с учетом лишь масштабного коэффициента. Планы испытаний, у которых масштабный коэффициент относительно нечувствителен к изменению предполагаемого распределения, могут оказаться крайне чувствительными при учете влияния фактической надежности. Иногда имеет место и обратный случай. [7]
В результате вычислений на основе этой модели могут быть найдены такие значения параметров форм документов, при которых критерий (3.2) достигает минимального значения при соблюдении ограничений. Математическая модель оптимизации строится на основе доступной, формализуемой исходной информации и обеспечивает проверку точности и подробности оптимизации. [8]
При рассмотрении этого рисунка можно заметить, что точки располагаются в определенном порядке в соответствии с углами Р2, и значениями Фг. Каждая из этих кривых располагается тем ниже, чем больше значение Р2л - Для колес с одинаковым углом ( 32л значение / ( тем больше, чем меньше значение параметра формы Ф Кривая для колес Р2л 90 представляет собой горизонтальную прямую. [9]
Как и следовало ожидать, анализ чувствительности при выборе плана испытаний на основе кривых риска по существу представляет повторение процесса выбора для нескольких значений параметра формы. На основе таких повторных выборов можно определить, каким образом изменяется стоимость испытаний в зависимости от выбранного параметра. Если стоимость нечувствительна к изменениям значения параметра формы, то в процессе выбора плана испытаний можно ограничиться грубой его оценкой. Однако если стоимость испытаний чувствительна к значению этого параметра, то следует приложить дополнительные усилия для получения разумных оценок параметра формы или воспользоваться более дорогими методами непараметрических испытаний. [10]
Другими словами, для каждого данного значения параметра формы существует свое масштабирование оси у. Это справедливо для гамма-распределения и распределения Вей-булла. Если исследователь не намерен вводить каких-либо пред положений относительно значения параметра формы, он может построить несколько шкал у по формуле (2.35), каждая из которых будет соответствовать определенному значению параметра формы. [11]
Следует указать, что для получения 6 - по формуле (2.35) должен быть известен параметр формы для распределения F ( и. Другими словами, для каждого данного значения параметра формы существует свое масштабирование оси у. Это справедливо для гамма-распределения и распределения Вей-булла. Если исследователь не намерен вводить каких-либо предположений относительно значения параметра формы, он может построить несколько шкал у по формуле (2.35), каждая из которых будет соответствовать определенному значению параметра формы. [12]
При описании поверхности каркасными моделями в прикладной геометрии вводится понятие определителя поверхности. Определитель поверхности включает совокупность условий, задающих поверхность. Определитель пространства состоит из двух частей: геометрической и алгоритмической. В геометрическую часть входят геометрические объекты, а также параметры формы и положения. Алгоритмическая часть определителя задается правилами построения точек и линий поверхности. Дискретное множество значений параметров формы и положения определяет дискретное множество линий поверхности, которое в свою очередь называется дискретным каркасом поверхности. Для получения непрерывного каркаса из дискретного необходимо произвести аппроксимацию поверхности. Непрерывные каркасы могут быть получены путем перемещения в пространстве плоской или пространственной линии. Такие геометрические модели называют кинематическими. [13]
Страницы: 1