Значение - безразмерный параметр
Cтраница 2
На рис. 1.2 приведены вычисленные по этой формуле значения угла контакта полимерного подшипника со стальным валом для наиболее часто встречающегося диапазона значений безразмерного параметра. Определив по этой формуле угол контакта 2фо, можно при необходимости найти по рис. 1.1 смещение вала. [16]
На рис. 6.3, 6.4 приведены зависимости между ф ( г) 6 - 4а и г, посчитанные для указанных выше значений безразмерных параметров соответственно для первой и второй задач. Из графиков видно, что с увеличением параметра Я величина контактных давлений под штампом будет уменьшаться. Нетрудно заметить, что когда жесткость нижнего слоя по отношению к верхнему велика, то контактные напряжения больше, чем в случае приведенных выше значений параметров пит при одном н том же Я. [17]
Если моделирование будет производиться в безразмерных переменных ( решение - на усмотрение студента и преподавателя), то произвести обезразмерива-ние и найти набор значений безразмерных параметров. [18]
В трубной гидравлике значение Re, при котором происходит смена режимов, равно ReKp 2320, в теории фильтрации закон Дарси имеет место при значении безразмерного параметра Re, меньшего критического ( ReKp), которое устанавливается из опыта. [19]
В работах Д. А. Эфроса показано, что при определенных условиях ( малые градиенты давления и перепады давления) фазовые проницаемости зависят не только от насыщенности, но и от значений безразмерных параметров л и яа. [20]
Конкретный вид зависимостей типа (6.25) может быть получен лишь в результате экспериментальных исследований процесса местного размыва от волн у отдельно стоящей опоры определенной формы и будет справедлив лишь в принятом диапазоне изменения значений безразмерных параметров, входящих в правую часть этих зависимостей. [21]
Значения безразмерного параметра а остаются неизменными. Это свидетельствует о нелинейности поведения каменной соли под большими нагрузками, требующей ее описания соответственно нелинейными уравнениями. [22]
Следовательно, уравнение состояния ( 127) правильно для веществ с достаточно большой массой, для которых Л становится пренебрежимо малой величиной и ее можно не учитывать. Значения безразмерных параметров в тройной и критической точках для инертных газов представлены в табл. 4, а температурные зависимости объемов и давлений показаны на рис. 23 и 24 соответственно. [24]
Для определения движения газа необходимо к системе уравнений (10.5), (10.6), (10.9) и (10.4) присоединить безразмерные граничные и начальные условия. Граничные условия сводятся к тому, что задаются значения безразмерных параметров или их производных на поверхностях, уравнения которых представлены в безразмерных координатах. Задание начальных условий означает, что в некоторый момент времени безразмерные параметры движения известны. Пусть рассматриваются два динамически подобных течения газа. Тогда границы этого течения будут геометрически подобны и подобно расположены, что входит в понятие динамического подобия, при этом безразмерные координаты в сходственных точках будут иметь одни и те же значения. [25]
В общем случае уравнение (2.135) является уравнением колебания. От соотношения между параметрами Т0 и 1 / а или, иначе, от значения безразмерного параметра T0a 2aL / c зависит характер колебательного процесса в трубопроводе. [26]
Задача состоит в их решении двумя отдельными шагами. Полученное таким образом наименьшее ( критическое) значение бифуркационной нагрузки для исследуемых кольцевых пластинок используется для определения некоторого значения безразмерного параметра, названного коэффициентом интенсивности нагружения а и определяемого как отношение текущего значения нагрузки к критической нагрузке потери устойчивости. Позднее для частных значений коэффициента а будут получены точные значения собственных частот колебаний для широкой области изменения числовых значений окружных волн. [27]
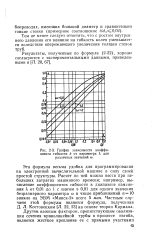 |
График зависимости коэффициента гибкости k от параметра К для различных значений о. [28] |
Эта формула весьма удобна для программирования на электронной вычислительной машине в силу своей простой структуры. Расчет по ней можно вести при небольших затратах машинного времени; например, вычисление коэффициентов гибкости в диапазоне изменения Я от 0 01 до 1 с шагом в 0 01 для одного значения безразмерного параметра со и числе приближений п10 заняло а ЭВМ Минск-2 всего 5 мин. [29]
Проанализируем теплоотдачу ребра с высотой Н м, толщиной sl мм, при длинах Ll; 5; 10 см и при бесконечно большой длине, если ребро выполнено из меди или стали. Тепловые параметры имеют следующие значения: Лм 380 вт / м град, Яст 45 вт / м град, а 10 вт / м2 - град. Значения безразмерного параметра KmL ломещены рядом. Следовательно, температура а конце медного ребра составляет все еще почти 94 % температуры основания, в то время как для стального ребра получается только 63 %, что обусловливает его худшую теплоотдачу. [30]
Страницы: 1 2 3
