Выходная реакция
Cтраница 1
Анализ выходных реакций при этом позволяет обнаружить грубые ошибки в монтаже или конструкции узлов и элементов. Наладочные тесты, как правило, используют при неавтоматизированном контроле. [1]
Измеяения выходной реакции, обусловленные изменяющимися частями коэффициентов, рассматриваются как возмущения, действующие на стационарную систему. [2]
Если для построения выходных реакций, импульсных переходных функций, переходных ошибок используется дискретное преобразование Лапласа то в ряде случаев оригинал удобно представить в виде ряда, составленного из ортогональных полиномов Гана. [3]
Изложенный метод определения выходных реакций нестационарных ДСАУ не требует нахождения корней характеристического уравнения; легко поддается алгоритмизации и, таким образом, удобен для случая, когда используются цифровые вычислительные машины. Выходной сигнал можно всегда найти с достаточной степенью точности, что достигается простым увеличением количества членов разложения. [4]
Рассмотрим метод расчета выходной реакции системы в случае, если переменные коэффициенты уравнений (1.5.1) и (1.5.2) могут быть представлены разложением в степенной ряд. [5]
Применение гармонич вычисления выходных реакции нелинейных систем. [6]
Формула (8.13) показывает, что выходная реакция фильтра с точностью до постоянного множителя выражает сумму автокорреляционной функции сигнала и взаимно корреляционной функции сигнала и помехи. Следовательно, реакция согласованного фильтра эквивалентна действию корреляционного приемника. [7]
Формула (8.13) показывает, что выходная реакция фильтра с точностью до постоянного множителя выражает сумму автокорреляционной функции сигнала и взаимно корреляционной функции сигнала и помехи. Следовательно, реакция согласованного фильтра эквивалентна действию корреляционного Приемника, которые возможно реализовать. [8]
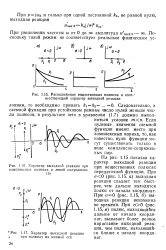 |
Расположение вещественных полюсов и соот-1 ветствующий характер выходной реакции.| Характер выходной реакции при комплексных полюсах в левой полуплоскости. [9] |
На рис. 1.15 показан характер выходной реакции при вещественных полюсах передаточной функции. При ст0 ( рис. 1.15, а) выходная реакция спадает тем быстрее, чем дальше находится полюс от начала координат. При ст0 ( рис. 1.15, б) выходная реакция неизменна во времени. При а0 ( рис. 1.15, в) полюс, находящийся дальше от начала координат, вызывает более резкое нарастание выходной реакции, чем полюс, находящийся ближе к началу координат. [10]
Сделаем обобщение разработанного алгоритма определения выходных реакций на класс многомерных систем автоматического управления, для которых процесс изменения коэффициентов системы дифференциальных уравнений допускает аппроксимацию степенными рядами. [11]
Вначале определим сощее изображение для сложной выходной реакции. Для этого к изображению процессов, полученному в предыдущем примере, следует прибавить изображение режима последействия. [12]
Вначале определим общее изображение для сложной выходной реакции. Для этого к изображению процессов, полученному в предыдущем примере, следует прибавить изображение режима последействия. [13]
Требуется получить систему высокого порядка, выходная реакция которой легко определяется. [14]
Как следует из уравнения (3.119), выходная реакция схемы определяется суперпозицией составляющих, зависящих от начальных условий и входных сигналов схемы. [15]
Страницы: 1 2 3 4