Установившаяся реакция

Cтраница 1

Установившаяся реакция на синусоидальное входное воздействие в общем случае является сложной функцией параметров преобразователя и описывается соответствующими амплитудно-частотной и фазочастотной характеристиками, которые могут быть получены в результате следующих математических действий. [1]

Установившуюся реакцию системы определяем методом комплексных амплитуд, известного также как метод механического импеданса, или метэд Эйлера. [2]

Установившуюся реакцию системы определяем методом комплексных амплитуд, известного также как метод механического импеданса, или метод Эйлера. [3]

Поскольку установившаяся реакция принята синусоидальной, постоянная интегрирования, определяющая величину свободной составляющей, отбрасывается. При наличии потерь в цепи свободная составляющая затухает. [4]

Если установившаяся реакция была получена таким образом, то импульсная реакция также может быть найдена на основе тех же данных. [5]

В установившейся реакции, в которой число цепей, образующихся в секунду, равно числу обрывающихся, количество1 радикалов НСЬ, образовавшихся и распавшихся за одну секунду, в одном кубическом сантиметре сосуда будет одинаковым. [6]

Расчет установившейся реакции на негармоническое периодическое воздействие выполняется методом гармонического анализа, в основу которого положен принцип наложения. При этом в качестве элементарных составляющих выбирают гармонических составляющих ряда Фурье, которыми приближенно изображают входное возмущение. Число учитываемых гармоник зависит от быстроты сходимости ряда и требуемой точности расчета. [7]

Таким образом, установившаяся реакция на гармоническое воздействие также представляет собой гармоническую функцию той же частоты со, амплитуда которой пропорциональна амплитуде входного возмущения и модулю передаточной функции цепи, а фаза ф ( ш) определяется аргументом этой функции. [8]

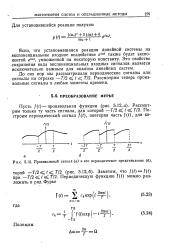Произвольный сигнал ( а и его периодическое представление ( б. [9]

Ясно, что установившаяся реакция линейной системы на экспоненциальное входное воздействие ег ш также будет экспо-нентой еш, умноженной на некоторую константу. Это свойство сохранения вида экспоненциальных входных сигналов является исключительно важным для анализа линейных систем. [10]

Звенья, обладающие установившейся реакцией (1.65), называют статическими. [11]

Схемы прямолинейных датчиков инерционного действия с преобразователями. [12]

Комплексные чувствительности позволяют найти установившуюся реакцию на измеряемую гармоническую величину. [13]

Здесь первое слагаемое является установившейся реакцией, а второе - свободной составляющей, которая зависит от начального тока и установившейся реакции. На рис. 5.1, в изображен график свободной составляющей, которая затухает по экспоненте от начального значения А до нуля. При t t значение тока равно А / е, так что постоянная времени численно равна промежутку времени, в течение которого экспоненциальная функция уменьшается в е раз. При t 2r и 3т экспонента уменьшается до е - 2 0 135 и e - 3 0 05 начального значения. Постоянная времени, определяющая быстроту спада свободной составляющей, для рассматриваемого контура тем больше, чем больше индуктивность, в которой запасается энергия, и чем меньше сопротивление, в котором энергия рассеивается. [14]

В некоторых случаях требуется получить решение для установившейся реакции не в виде ряда, а в замкнутой форме. Рассмотрим одно из возможных решений с использованием преобразования Лапласа. [15]

Страницы: 1 2 3 4