Значение - случайный процесс
Cтраница 4
При выводе (4.25) учтено, что математическое ожидание произведения двух нецентрированных случайных процессов равно произведению их математических ожиданий плюс корреляционный момент между их центрированными составляющими. Поскольку здесь перемножаются значения одного и того же процесса при разных значениях его аргумента, данный корреляционный момент равен автокорреляционной функции этого процесса при аргументе, равном разности аргументов перемножаемых значений случайного процесса. [46]
 |
Типичные корреляционные функции. [47] |
Из рис. 14.5 видно, что с увеличением т взаимосвязь между X ( f) и X ( t г) ослабевает и корреляционная функция уменьшается. Наличие отрицательных значений корреляционных функций ( см. рис. 14.5, б, в) указывает на то, что в структуре случайного процесса присутствует периодичность, в связи с чем наблюдается отрицательная корреляция между значениями случайного процесса: положительным отклонениям от среднего в одном сечении соответствуют через определенный промежуток времени отрицательные отклонения в другом сечении, и наоборот. [48]
 |
Типичные корреляционные функции. [49] |
Из рис. 14.5 видно, что с увеличением т взаимосвязь между X ( t) и X ( t т) ослабевает и корреляционная функция уменьшается. Наличие отрицательных значений корреляционных функций ( см. рис. 14.5, б, в) указывает на то, что в структуре случайного процесса присутствует периодичность, в связи с чем наблюдается отрицательная корреляция между значениями случайного процесса: положительным отклонениям от среднего в одном сечении соответствуют через определенный промежуток времени отрицательные отклонения в другом сечении, и наоборот. [50]
Случайный процесс, моделирующий график нагрузки заводской сети, с вполне достаточной точностью можно считать марковским процессом, что имеет следующий смысл. Пусть реализация случайного процесса уже осуществилась на некотором начальном интервале времени ( t0, ti); очевидно, что в соответствии с характером корреляционных связей этого процесса последующее случайное продолжение реализации при t ti будет зависеть от значений Р - ( 0 полученных для t ti, но не зависит от значений Pf ( t) при t to, что объясняется затуханием корреляционных связей между двумя значениями случайного процесса при увеличении интервала т между ними. [51]
Охарактеризуем кратко особенности содержания настоящей книги. В книге выделена глава ( первая), посвященная случайным процессам в широком смысле. Так мы назвали ту часть теории случайных процессов, которая имеет дело лишь с распределениями конечных наборов значений случайного процесса. [52]
 |
Реализации случайных процессов. [53] |
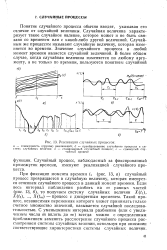
Понятие случайного процесса обычно вводят, указывая его отличие от случайной величины. Случайная величина характеризует такое случайное явление, которое может и не быть связано со временем или с какой-либо другой величиной. Случайным же процессом называют случайную величину, которая изменяется во времени. Значение случайного процесса в любой момент времени является случайной величиной. [54]
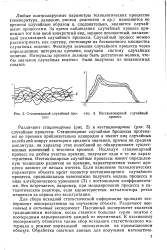 |
Стационарный случайный про - нис. 3. Нестационарный случайный цесс процесс. [55] |
Любые контролируемые параметры технологических процессов ( температура, давление, расход реагентов и др.) изменяются во времени случайным образом и, следовательно, являются случайными процессами. За время наблюдения случайный процесс принимает тот или иной конкретный вид, заранее неизвестный, называемый реализацией случайного процесса. Фиксируя значения случайного процесса через определенные интервалы времени, получаем систему случайных величин. Интервалы времени должны быть достаточно велики, чтобы значения случайных величин были получены из независимых опытов. [56]
 |
Стационарный случайный процесс. [57] |
Любые контролируемые параметры технологических процессов ( температура, давление, расход реагентов и др.) изменяются во времени случайным образом и, следовательно, являются случайными процессами. За время наблюдения случайный процесс при-цимает тот или иной конкретный вид, заранее неизвестный, называемый реализацией случайного процесса. Фиксируя значения случайного процесса через определенные интервалы времени, получаем систему случайных величин. Интервалы времени должны быть достаточно велики, чтобы значения случайных величин были получены из независимых опытов. [58]
Страницы: 1 2 3 4