Численная реализация - модель
Cтраница 1
Численная реализация модели на персональном компьютере несложна. Многочисленные расчеты показали, что качественную картину процесса консолидации ( сценарий) определяют главным образом три фактора: характер неоднородности ( величина ртах или ртт); сооношенис между vb и К; расстояние от зоны / / до верхней и нижней границ сжимаемой зоны. [1]
Численная реализация моделей течений, учитывающих неравновесные эффекты, сводится к решению смешанных нелинейных краевых задач для систем уравнений в частных производных высокого порядка с малыми параметрами перед старшими производными, и представляет собой сложную проблему. Кроме того, решения должны быть получены в областях, в которых наряду с подобластями гладких течений содержатся зоны резких неоднородностей типа ударных волн, пограничных слоев и с заранее неизвестными границами. Все это требует разработки и применения эффективных численных и аналитических методов исследования таких задач. [2]
Численная реализация моделей течений, учитывающих неравновесные эффекты, сводится к решению смешанных нелинейных краевых задач для систем уравнений в частных производных высокого порядка с малыми параметрами перед старшими производными, и представляет собой сложную проблему. Кроме того, решения должны быть получены в областях, в которых наряду с подобластями гладких течений содержатся зоны резких неоднородностеи типа ударных волн, пограничных слоев и с заранее неизвестными границами. Все это требует разработки и применения эффективных численных и аналитических методов исследования таких задач. [3]
После численной реализации модели оптимизации полезно провести анализ результатов с целью оценки, например, устойчивости полученного решения относительно возможных вариаций параметров проекта. Это тем более важно в случае многокритериальных постановок задач оптимизации, поскольку высокая чувствительность оптимального проекта конструкции к вариациям по некоторой группе параметров может приводить в реальной конструкции к существенно иным значениям частных показателей эффективности по сравнению с результатами расчета. Если по итогам такого анализа оптимальное решение признается неустойчивым, то, по-видимому, соответствующий проект конструкции не может быть признан достаточно эффективным. [4]
При численной реализации модели среды вид уравнения (2.52), являющегося скалярным, в лагранжевой системе координат не изменяется по мере движения сетки вместе со средой, в то время как вид уравнения (2.53) изменяется, так как оно тензорное. Чтобы учесть этот эффект, в работах [40, 44, 45] вводятся поправки, связанные с вращением ячейки как целого. [5]
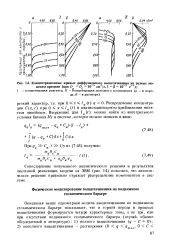 |
Концентрационные кривые диффузионного выщелачивания на разные моменты времени ( при D - Рс 10 5 см2 / с, k J3 10 2 с 1. [6] |
Сопоставление полученного аналитического решения и результатов численной реализации модели на ЭВМ ( рис. 14) показало, что аналитическое решение правильно отражает распределение компонентов в системе. [7]
На третьем этапе процесса ОПК, как следует из изложенного, осуществляется численная реализация модели оптимизации. При этом в случае многокритериальной задачи оптимизации исходная векторная модель оптимизации должна быть предварительно преобразована к скалярному виду, в котором по определенному правилу вектору эффективности Е ставится в соответствие некоторый интегральный показатель эффективности, так называемый целевой функционал, или целевая функция. [8]
Заметим, что сформулированная модель обладает гомоморфизмом s - - s, поэтому численная реализация модели проведена с использованием метода ОСП. [9]
Однако для течений, в которых ударная волна становится тонкой ( большие числа Рейнольдса), в численной реализации модели параболизованных уравнений Навье-Стокса возникают объективные трудности, связанные с появлением внутри ударной волны очень больших градиентов искомых функций. [10]
Отображение процессов добычи нефти и подготовки запасов на каждой стадии в единой экономико-математической модели в принципе возможно, однако учет нелинейных зависимостей, существующих между отдельными технологическими и экономическими показателями этих процессов, а также возрастание размерности задачи затрудняют численную реализацию модели такого вида. Преодолеть эту трудность позволяет разделение моделей Mi на два взаимосвязанных блока: формирования вариантов добычи - нефти и формирования вариантов подготовки запасов. [11]
Таким образом, получаем 13 вариантов допустимых по проектной ситуации конструкционных материалов. Совершенно очевидно, что модель оптимизации может быть сформулирована только для гибридного композита и, таким образом, содержать в качестве параметров оптимизации две интенсивности армирования, одна из которых в результате численной реализации модели может принять нулевое значение. [12]
В главах 5 и 6 рассмотрены гидродинамическая и гибридная модели течения плазмы в окрестности плоского нейтрального слоя. Приведены результаты численного решения нестационарных двумерных задач динамики пересоединения силовых линий магнитного поля, исследована зависимость характеристик течения от параметров плазмы и внешнего возмущения. Представлены алгоритмы численной реализации моделей. [13]
Здесь модель месторождения составляет часть модели нефтедобывающего района. Ее основные параметры связывают объемы добычи нефти на месторождении с фондом и динамикой бурения эксплуатационных скважин, что обеспечивает решение модели в соответствии с реальными закономерностями развития буровых мощностей. Вместе с тем это затрудняет численную реализацию районной модели, так как большое число месторождений, входящих в район, обусловливает значительный рост ее размерности. Кроме того, в работе [63] отсутствуют зависимости дебитов скважин от характеров способов разработки, что сужает число возможных вариантов. [14]
Поскольку возможности численного моделирования ограничиваются конечной областью, то правильность получаемых результатов будет определяться тем, насколько удачно выбраны фиктивные границы области исследования. Величины гп и / m подбираются так, чтобы на соответствующих участках границы области можно было пренебречь возмущающим влиянием скважины и поверхности грунта. Их выбор зависит от условий конкретной задачи и может варьироваться в широких пределах, определяемых разумным ограничением на размеры необходимой для численной реализации модели памяти ЭВМ и в конечном итоге приемлемой скоростью расчета. [15]
Страницы: 1