Ребро - октаэдр
Cтраница 1
Ребро октаэдра равно а. [1]
Чему равно отношение ребра октаэдра, вписанного в куб, к ребру этого куба. [2]
Чтобы выбранные на ребрах октаэдра точки деления были - вершинами правильного икосаэдра, необходимо, чтобы и 12 равнобедренных треугольников, служащие гранями нового многогранника, обратились в равносторонние треугольники. [3]
 |
Элементы структуры силикатов с мелкими ( а и крупными ( б катионами ( тетраэдры [ SiO4 ] заштрихованы. [4] |
Эта длина несколько больше ребра октаэдра, что заставляет диортогруппу изгибаться вокруг октаэдра катиона. [5]
В ней колонки сопряженных ребрами крестообразно уложенных октаэдров сочленяются друг с другом вершинами. [6]
Эти цепи затем соединяются вершинами или ребрами октаэдров, так что возникают каналы, сечения которых имеют форму параллелограмма или треугольника. В трехгранных каналах размещаются группы [ Si2O7 ], в которых тетраэдры [ SiO4 ] повернуты друг относительно друга аналогично тетраэдрам ZnO. [7]
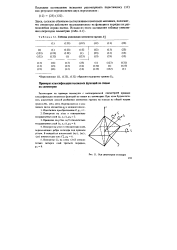 |
Оси симметрии октаэдра. [8] |
Поворот на угол тт относительно осей, пересекающих ребра октаэдра под прямым углом. [9]
Кубические кристаллы построены из попарно сопряженных по ребру октаэдров; фрагменты Re2Oio ( рис. 50), в свою очередь, сочленяются по вершинам и образуют каркас с крупными пустотами, занятыми атомами лантана. [10]
 |
Кристаллическое строение ( структурные типы моногалогенидов индня и таллия. [11] |
Направление неподеленной пары вдоль оси 2-го порядка к середине ребра октаэдра вызывает удлинение последнего; если же электронная пара расположена вдоль оси 3-го порядка искажение октаэдра сопровождается увеличением размера одной из его граней. [12]
В некоторых случаях включенные в магнетит иголочки рутила располагаются параллельно ребрам октаэдра. [13]
Если соединить б точек между собой кратчайшими прямыми, то образуются ребра октаэдра. В трех последних случаях эта фигура даляется только псевдооктаэдром. Конечно, возможны еще и другие случаи снижения симметрии, однако, как и в последних примерах псевдотетраэдра, 6 точек становятся отчасти неэквивалентными, так что точечная конфигурация оказывается сложной. [14]
Если соединить б точек между собой кратчайшими прямыми, то образуются ребра октаэдра. В трех последних случаях эта фигура является только псевдооктаэдром. Конечно, возможны еще и другие случаи снижения симметрии, однако, как и в последних примерах псевдотетраэдра, б точек становятся отчасти неэквивалентными, так что точечная конфигурация оказывается сложной. [15]
Страницы: 1 2 3 4